
【题目】如图,![]() 是
是![]() 的直径,且
的直径,且![]() ,点
,点![]() 均在
均在![]() 上,
上,![]() 的延长线交
的延长线交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,
,![]() .
.
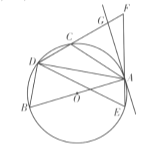
(1)求证:![]() .
.
(2)填空:
①当![]() __________,
__________,![]() 是等腰直角三角形;
是等腰直角三角形;
②当![]() __________,四边形
__________,四边形![]() 是平行四边形.
是平行四边形.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
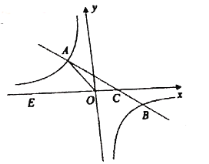
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() (
(![]() )的图象与反比例函数
)的图象与反比例函数![]() (
(![]() )的图象交于二、四象限内的
)的图象交于二、四象限内的![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 的坐标为
的坐标为![]() .线段
.线段![]() ,
,![]() 为
为![]() 轴上一点,
轴上一点,![]() ,
,![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中顶点为点M的抛物线是由抛物线![]() 向右平移1个单位得到的,它与y轴负半轴交于点A,点B在抛物线上,且横坐标为3.
向右平移1个单位得到的,它与y轴负半轴交于点A,点B在抛物线上,且横坐标为3.
![]() 写出以M为顶点的抛物线解析式.
写出以M为顶点的抛物线解析式.
![]() 连接AB,AM,BM,求
连接AB,AM,BM,求![]() ;
;
![]() 点P是顶点为M的抛物线上一点,且位于对称轴的右侧,设PO与x正半轴的夹角为
点P是顶点为M的抛物线上一点,且位于对称轴的右侧,设PO与x正半轴的夹角为![]() ,当
,当![]() 时,求点P坐标.
时,求点P坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=6,将此矩形绕点B顺时针方向旋转θ(0<θ<180°)得到矩形A1BC1D1,直线BA1、C1D1分别与直线CD相交于点E、F.
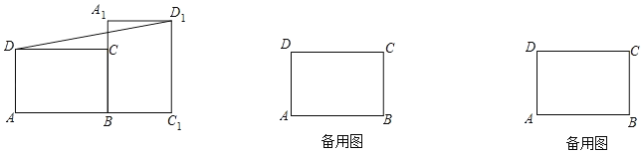
(1)若此矩形绕点B顺时针方向旋转90°,求DD1的长;
(2)在旋转过程中,点D、A1、D1三点共线时,求△BCE的面积;
(3)在矩形ABCD旋转的过程中,是否存在某个位置使得以B、E、F、D1为顶点的四边形为平行四边形?若存在,求出CF的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在今年2月底以每袋23元的成本价收购一批农产品准备向外销售,当此农产品售价为每袋36元时,3月份销售125袋,4、5月份该农产品十分畅销,销售量持续走高.在售价不变的基础上,5月份的销售量达到180袋.设4、5这两个月销售量的月平均增长率不变.
(1)求4、5这两个月销售量的月平均增长率;
(2)6月份起,该商店采用降价促销的方式回馈顾客,经调查发现,该农产品每降价1元/袋,销量就增加4袋,当农产品每袋降价多少元时,该商店6月份获利1920元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上的点,
上的点,![]() 是线段
是线段![]() 上的点,且
上的点,且![]() .
.
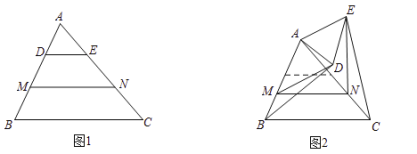
(1)观察猜想
如图1,若点![]() 是线段
是线段![]() 的三等分点,则
的三等分点,则![]() __________,
__________,![]() ___________.由此,我们猜想线段
___________.由此,我们猜想线段![]() ,
,![]() ,
,![]() ,
,![]() 之间满足的数量关系是_________.
之间满足的数量关系是_________.
(2)类比探究
将![]() 在平面内绕点
在平面内绕点![]() 按逆时针方向旋转一定的角度,连接
按逆时针方向旋转一定的角度,连接![]() ,
,![]() ,
,![]() ,
,![]() ,猜想在旋转的过程中,(1)中的结论是否仍然成立?若成立,请仅就图2的情形给出证明;若不成立,请说明理由.
,猜想在旋转的过程中,(1)中的结论是否仍然成立?若成立,请仅就图2的情形给出证明;若不成立,请说明理由.
(3)解决问题
将![]() 在平面内绕点
在平面内绕点![]() 自由旋转,若
自由旋转,若![]() ,请直接写出线段
,请直接写出线段![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
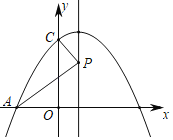
【题目】如图,抛物线y=﹣![]() x2+
x2+![]() x+3与x轴交于点A,B(点A在点B的左边),交y轴于点C,点P为抛物线对称轴上一点.则△APC的周长最小值是_____.
x+3与x轴交于点A,B(点A在点B的左边),交y轴于点C,点P为抛物线对称轴上一点.则△APC的周长最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
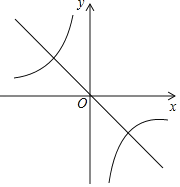
【题目】反比函数![]() 的图象如图所示.
的图象如图所示.
(1)求m的值;
(2)当x>﹣1时,y的取值范围是 ;
(3)当直线y2=﹣x与双曲线![]() 交于A、B两点(A在B的左边)时,结合图象,求出在什么范围时y2>y1?
交于A、B两点(A在B的左边)时,结合图象,求出在什么范围时y2>y1?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 与点
与点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 是
是![]() 轴上的一个动点,设点
轴上的一个动点,设点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() 交抛物线于点
交抛物线于点![]() .
.
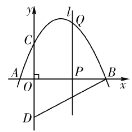
(1)求点![]() ,点
,点![]() ,点
,点![]() 的坐标;
的坐标;
(2)求直线![]() 的解析式;
的解析式;
(3)在点![]() 的运动过程中,是否存在点
的运动过程中,是否存在点![]() ,使
,使![]() 是以
是以![]() 为直角边的直角三角形?若存在,求出点
为直角边的直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com