
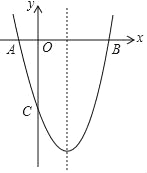
【题目】如图,抛物线y=ax2+bx﹣3(a≠0)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,且BO=OC=3AO.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PBC是等腰三角形?若存在,请直接写出符合条件的点P坐标;若不存在,请说明理由.
【答案】(1)y=x2﹣2x﹣3;(2)存在,理由见解析;符合条件的P点坐标为P(1,﹣1)或P(1,![]() )或P(1,﹣
)或P(1,﹣![]() )或P(1,﹣3+
)或P(1,﹣3+![]() )或P(1,﹣3﹣
)或P(1,﹣3﹣![]() ).
).
【解析】
(1)先求出点C的坐标,在由BO=OC=3AO,确定出点B,A的坐标,最后用待定系数法求出抛物线解析式.
2)设出点P的坐标,表示出PB,PC,求出BC,分三种情况利用两边相等建立方程求解即可.
(1)∵抛物线y=ax2+bx﹣3,
∴c=﹣3,
∴C(0,﹣3),
∴OC=3,
∵BO=OC=3AO,
∴BO=3,AO=1,
∴B(3,0),A(﹣1,0),
∵该抛物线与x轴交于A、B两点,
∴![]() ,
,
∴![]() ,
,
∴抛物线解析式为y=x2﹣2x﹣3,
(2)存在,
理由:设P(1,m),
∵B(3,0),C(0,﹣3),
∴BC=3![]() ,PB=
,PB=![]() ,PC=
,PC=![]() ,
,
∵△PBC是等腰三角形,
①当PB=PC时,
∴![]() =
=![]() ,
,
∴m=﹣1,
∴P(1,﹣1),
②当PB=BC时,
∴3![]() =
=![]() ,
,
∴m=±![]() ,
,
∴P(1,![]() )或P(1,﹣
)或P(1,﹣![]() ),
),
③当PC=BC时,
∴3![]() =
=![]() ,
,
∴m=﹣3±![]() ,
,
∴P(1,﹣3+![]() )或P(1,﹣3﹣
)或P(1,﹣3﹣![]() ),
),
∴符合条件的P点坐标为P(1,﹣1)或P(1,![]() )或P(1,﹣
)或P(1,﹣![]() )或P(1,﹣3+
)或P(1,﹣3+![]() )或P(1,﹣3﹣
)或P(1,﹣3﹣![]() ).
).


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图所示的折线是某个函数的图象,根据图象解答下列问题.
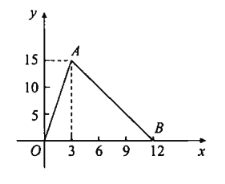
(1)写出自变量x的取值范围:__________,函数值y的取值范围:__________;
(2)求这个分段函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
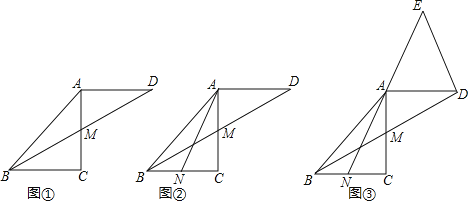
【题目】已知△ABC是等腰直角三角形,∠C=90°,点M是AC的中点,延长BM至点D,使DM=BM,连接AD.
(1)如图①,求证:△DAM≌△BCM;
(2)已知点N是BC的中点,连接AN.
①如图②,求证:△BCM≌△ACN;
②如图③,延长NA至点E,使AE=NA,连接DE.求证:BD⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)小慧和小聪沿图1中的景区公路游览.小慧乘坐车速为30km/h的电动汽车,早上7:00从宾馆出发,游玩后中午12:00回到宾馆.小聪骑车从飞瀑出发前往宾馆,速度为20km/h,途中遇见小慧时,小慧恰好游完一景点后乘车前往下一景点.上午10:00小聪到达宾馆.图2中的图象分别表示两人离宾馆的路程s(km)与时间t(h)的函数关系.试结合图中信息回答:

(1)小聪上午几点钟从飞瀑出发?
(2)试求线段AB、GH的交点B的坐标,并说明它的实际意义.
(3)如果小聪到达宾馆后,立即以30km/h的速度按原路返回,那么返回途中他几点钟遇见小慧?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义运算a![]() b=a(1-b),下面给出了关于这种运算的四个结论:
b=a(1-b),下面给出了关于这种运算的四个结论:
①2![]() (-2)=6 ②a
(-2)=6 ②a![]() b=b
b=b![]() a
a
③若a+b=0,则(a![]() a)+(b
a)+(b![]() b)=2ab ④若a
b)=2ab ④若a![]() b=0,则a=0.
b=0,则a=0.
其中正确结论的序号是 (填上你认为所有正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上.顶点B的坐标为(3,![]() ),点C的坐标为(1,0),且∠AOB=30°点P为斜边OB上的一个动点,则PA+PC的最小值为( )
),点C的坐标为(1,0),且∠AOB=30°点P为斜边OB上的一个动点,则PA+PC的最小值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
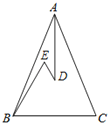
【题目】如图所示,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC≡∠E=60°,若BE=10,DE=4,则BC的长度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市场上甲种商品的采购价为60元/件,乙种商品的采购价为100元/件,某商店需要采购甲、乙两种商品共15件,且乙种商品的件数不少于甲种商品件数的2倍.设购买甲种商品![]() 件(
件(![]() >0),购买两种商品共花费
>0),购买两种商品共花费![]() 元.
元.
(1)求出![]() 与
与![]() 的函数关系式(写出自变量
的函数关系式(写出自变量![]() 的取值范围);
的取值范围);
(2)试利用函数的性质说明,当采购多少件甲种商品时,所需要的费用最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com