
【题目】对称变换和平移变换在平面几何中有着广泛的应用,特别是在解决有关最值问题时,更是我们常用的思维方法,请你利用所学知识解决下列问题:

(1)如图①,在平面直角坐标系中,已知点A(0,1),点B(2,1),点P在x轴上运动,当PA+PB的值最小时,点P的坐标是 ;(请直接写出答案)
(2)如图②,AD⊥l于点D,BC⊥l于点C,且AD=2,AB=BC=4,当点P在直线l上运动时,PA+PB的最小值是 ;(请直接写出答案)
(3)如图③,直线a∥b,且a与b之间的距离为1,点A到直线a的距离为2,点B到直线b的距离为2,且AB=![]() ,问:在直线a上是否存在点C,在直线b上是否存在点D,使得CD⊥a,且AC+CD+DB的值最小?若存在,请求出AC+CD+DB的最小值;若不存在,请说明理由.
,问:在直线a上是否存在点C,在直线b上是否存在点D,使得CD⊥a,且AC+CD+DB的值最小?若存在,请求出AC+CD+DB的最小值;若不存在,请说明理由.
(4)如图④,在平面直角坐标系中,A(6,0),B(6,4),线段CD在直线y=x上运动,且CD=2![]() ,则四边形ABCD周长的最小值是 ,此时点D的坐标为 .(请直接写出答案)
,则四边形ABCD周长的最小值是 ,此时点D的坐标为 .(请直接写出答案)
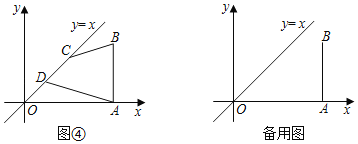
【答案】(1)(1,0);(2)4![]() ;(3)存在,6;(4)6
;(3)存在,6;(4)6![]() +4,(3,3)
+4,(3,3)
【解析】
(1)如图1,作点A关于x轴的对称点![]() ,连接
,连接![]() 交x轴于点P,则点P为所求点,然后利用待定系数法求出直线
交x轴于点P,则点P为所求点,然后利用待定系数法求出直线![]() 的解析式,然后令
的解析式,然后令![]() 即可求出x的值,从而可确定P的坐标;
即可求出x的值,从而可确定P的坐标;
(2)如图2,作点A关于直线l的对称点![]() ,连接
,连接![]() 交直线l于点P,则点P为所求点,利用矩形的性质和勾股定理进而求解即可;
交直线l于点P,则点P为所求点,利用矩形的性质和勾股定理进而求解即可;
(3)如图3,将点A向下平移1个单位得到![]() ,连接
,连接![]() 交直线b于点D,过点D作DC⊥a于点C,连接AC,则点C、D为所求点,然后利用勾股定理求出
交直线b于点D,过点D作DC⊥a于点C,连接AC,则点C、D为所求点,然后利用勾股定理求出![]() 的长度,进而求解;
的长度,进而求解;
(4)如图4,将点A沿y=x方向向右平移2![]() 个单位得到
个单位得到![]() ,作点
,作点![]() 关于直线y=x的对称点
关于直线y=x的对称点![]() ,连接
,连接![]() 交直线y=x于点C,将点C沿直线向下平移2
交直线y=x于点C,将点C沿直线向下平移2![]() 个单位得到点C,则点C、D为所求点,首先利用平行四边形的性质得出四边形ABCD周长=4+2
个单位得到点C,则点C、D为所求点,首先利用平行四边形的性质得出四边形ABCD周长=4+2![]() +
+![]() 为最小,然后利用勾股定理即可求出
为最小,然后利用勾股定理即可求出![]() 的值,进而可求出周长的最小值,然后利用待定系数法求出直线
的值,进而可求出周长的最小值,然后利用待定系数法求出直线![]() 的解析式,进而可求出C的坐标,从而D的坐标可求 .
的解析式,进而可求出C的坐标,从而D的坐标可求 .
解:(1)如图1,作点A关于x轴的对称点![]() ,连接
,连接![]() 交直线l于点P,则点P为所求点,
交直线l于点P,则点P为所求点,

∵点![]() 、A关于x轴对称,
、A关于x轴对称,![]() ,
,
![]() ,
,![]() ,
,
∴![]() 为最小;
为最小;
设直线![]() 的表达式为:y=kx+b,
的表达式为:y=kx+b,
将点![]() 代入得
代入得
![]() ,解得:
,解得:![]() ,
,
故直线![]() 的表达式为:y=x﹣1,
的表达式为:y=x﹣1,
当y=0时,x=1,故点P(1,0);
故答案为:(1,0);
(2)如图2,作点A关于直线l的对称点![]() ,连接
,连接![]() 交直线l于点P,则点P为所求点,过点
交直线l于点P,则点P为所求点,过点![]() 作
作![]() 交BC的延长线于点H,
交BC的延长线于点H,

∵点![]() 、A关于x轴对称,
、A关于x轴对称,
![]() ,
,
∴![]() 为最小;
为最小;
过点A作AM⊥BC于点M,
![]() ,
,
∴![]() ,
,
∴四边形ADCM是矩形,
∴![]() ,
,
同理,![]() ,
,
∴BM=BC﹣CM=BC﹣AD=4﹣2=2.
在Rt△ABM中,AM2=AB2﹣BM2=16﹣4=12=![]() ,
,
BH=CH+BC=![]() +BC=2+4=6,
+BC=2+4=6,
在![]() 中,
中,
![]() ;
;
即PA+PB的最小值为4![]() ,
,
故答案为:4![]() ;
;
(3)存在,理由:
如图3,将点A向下平移1个单位得到![]() ,连接
,连接![]() 交直线b于点D,过点D作DC⊥a于点C,连接AC,则点C、D为所求点,
交直线b于点D,过点D作DC⊥a于点C,连接AC,则点C、D为所求点,

∵![]() ,且
,且![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∴![]() 为最小.
为最小.
过点![]() 、A分别作直线a的平行线,分别交过点B与a的垂线于点G、H,则四边形
、A分别作直线a的平行线,分别交过点B与a的垂线于点G、H,则四边形![]() 为矩形,
为矩形,
∵BH=2+1+2=5,AB=![]() ,则AH=
,则AH=![]() =3,
=3,
在![]() 中,
中,![]() ,BG=2+1+1=4,
,BG=2+1+1=4,
![]() ,
,
∴![]() ,
,
∴AC+CD+DB最小值为6;
(4)如图4,将点A沿y=x方向向右平移2![]() 个单位长度得到
个单位长度得到![]() ,作点
,作点![]() 关于直线y=x的对称点
关于直线y=x的对称点![]() ,连接
,连接![]() 交直线y=x于点C,将点C沿直线向下平移2
交直线y=x于点C,将点C沿直线向下平移2![]() 个单位长度得到点D,则点C、D为所求点.
个单位长度得到点D,则点C、D为所求点.
连接AD、![]() ,
,

设C的坐标为![]() ,
,
∵![]() ,
,
![]() ,
,
![]() ,
,
∴如果沿着直线![]() 向上平移
向上平移![]() 个单位长度,相当于向右平移2个单位,再向上平移2个单位.
个单位长度,相当于向右平移2个单位,再向上平移2个单位.
∵![]() ,
,
![]() .
.
∵点![]() 和点
和点![]() 关于
关于![]() 对称,
对称,
![]() .
.
∵![]() ,
,
∴四边形![]() 为平行四边形,
为平行四边形,
∴![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
∴四边形ABCD周长=AB+CD+BC+AD=AB+CD+BC+![]() =4+2
=4+2![]() +
+![]() 为最小.
为最小.
∵![]() =
=![]() =4
=4![]() ,
,
故四边形ABCD周长最小值为:6![]() 4.
4.
设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 代入解析式中得
代入解析式中得
![]() 解得
解得![]()
∴直线![]() 解析式为
解析式为![]() .
.
![]() ,解得:
,解得:![]() ,
,
故点C(5,5),
而CD=2![]() ,
,
∴点D可以看成点C向左平移2个单位长度,再向下平移2个单位长度得到的,
∴点D(3,3),
故答案为:6![]() +4;(3,3).
+4;(3,3).


科目:初中数学 来源: 题型:
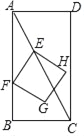
【题目】如图,在矩形ABCD中,AB=4,BC=2,点E从点A出发,以每秒![]() 个单位长度的速度沿对角线AC向终点C运动,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F顺时针旋转90°得到线段FG,以EF,FG为边作正方形EFGH,设点E运动的时间为t秒(t>0).
个单位长度的速度沿对角线AC向终点C运动,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F顺时针旋转90°得到线段FG,以EF,FG为边作正方形EFGH,设点E运动的时间为t秒(t>0).
(1)用含t的代数式表示点E到边AB的距离.
(2)当点G落在边AB上时,求t的值.
(3)连结BG,设△BFG的面积为S平方单位(S>0),求S与t之间的函数关系式.
(4)直接写出当正方形EFGH的顶点与点B,D距离相等时的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=6,BC=8,动点P从A点出发,以1cm/s的速度,沿A—C—B向B点运动,同时,动点Q从C点出发,以2cm/s的速度,沿C—B—A向A点运动,当其中一点运动到终点时,两点同时停止运动。设运动时间为t秒,当t=_______秒时,△PCQ的面积等于8cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=90°,AD=CD+AB,∠BAC=45°,E是BC上一点,且∠DAE=45°,若BC=8,则△ADE面积为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=10,AC=2![]() ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.
【答案】10或6
【解析】试题解析:根据题意画出图形,如图所示,

如图1所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD-CD=8-2=6,
则BC的长为6或10.
【题型】填空题
【结束】
12
【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年1月,市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价.评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生进行问卷调查,了解他们每天在课外用于学习的时间,并绘制成如下不完整的统计图. 根据上述信息,解答下列问题:

(1)本次抽取的学生人数是 ______ ;扇形统计图中的圆心角α等于 ______ ;补全统计直方图;
(2)被抽取的学生还要进行一次50米跑测试,每5人一组进行.在随机分组时,小红、小花两名女生被分到同一个小组,请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=ax+b(a、b是常数,a≠0)函数图象经过(﹣1,4),(2,﹣2)两点,下面说法中:(1)a=2,b=2;(2)函数图象经过(1,0);(3)不等式ax+b>0的解集是x<1;(4)不等式ax+b<0的解集是x<1;正确的说法有____________________.(请写出所有正确说法的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
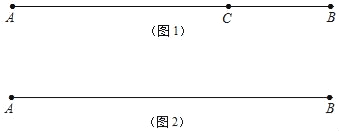
【题目】(探索新知)
如图1,点C在线段AB上,图中共有3条线段:AB、AC和BC,若其中有一条线段的长度是另一条线段长度的两倍,则称点C是线段AB的“二倍点”.
(1)一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
(深入研究)
如图2,若线段AB=20cm,点M从点B的位置开始,以每秒2cm的速度向点A运动,当点M到达点A时停止运动,运动的时间为t秒.
(2)问t为何值时,点M是线段AB的“二倍点”;
(3)同时点N从点A的位置开始,以每秒1cm的速度向点B运动,并与点M同时停止.请直接写出点M是线段AN的“二倍点”时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注.某单位计划在室内安装空气净化装置,需购进A、B两种设备.每台B种设备价格比每台A种设备价格多0.7万元,花3万元购买A种设备和花7.2万元购买B种设备的数量相同.
(1)求A种、B种设备每台各多少万元?
(2)根据单位实际情况,需购进A、B两种设备共20台,总费用不高于15万元,求A种设备至少要购买多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com