
分析 将等式a2+b2+c2+200=12a+16b+20c变形得(a-6)2+(b-8)2+(c-10)2=0,从而求出a、b、c的值,然后判断△ABC的形状并求其面积.
解答 解:∵△ABC的三边满足a2+b2+c2+200=12a+16b+20c
∴a2+b2+c2-12a-16b-20c+200=0
∴(a2-12a+36)+(b2-16a+64)+(c2-20c+100)=0
∴(a-6)2+(b-8)2+(c-10)2=0
∴a=6,b=8,c=10,
又∵102=82+62,即:c2=a2+b2,
∴△ABC是直角三角形,且c为斜边
∴S△ABC=$\frac{1}{2}ab$=$\frac{1}{2}×6×8$=24
即:△ABC的面积为24
点评 本题考查了因式分解的应用问题,解题的关键是能够将等式a2+b2+c2+200=12a+16b+20c变形为(a-6)2+(b-8)2+(c-10)2=0,并根据非负数的和为0 求出三边的长.


科目:初中数学 来源: 题型:选择题
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年湖北省枝江市九校七年级3月联考数学试卷(解析版) 题型:单选题
已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1 与∠2的关系一定成立的是( )
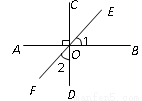
A. 相等 B. 互余 C. 互补 D. 互为对顶角
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
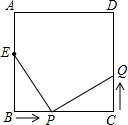 如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.如果点P在线段BC上以2cm/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动,设运动的时间为t秒,
如图,已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm.如果点P在线段BC上以2cm/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动,设运动的时间为t秒,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
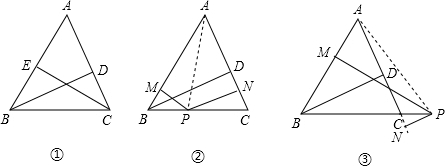
 如图,等边△ABC的边长为2,且DB=DC,∠BDC=120°,现有∠MDN=60°,其两边分别与AB,AC交于点M,N,连接MN,将∠MDN绕着D点旋转,使得M,N始终在边AB和边AC上.试判断在这一过程中,△AMN的周长是否发生变化,若没有变化,请求出其周长;若发生变化,请说明理由.
如图,等边△ABC的边长为2,且DB=DC,∠BDC=120°,现有∠MDN=60°,其两边分别与AB,AC交于点M,N,连接MN,将∠MDN绕着D点旋转,使得M,N始终在边AB和边AC上.试判断在这一过程中,△AMN的周长是否发生变化,若没有变化,请求出其周长;若发生变化,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com