
| A | B | C | |
| 笔试 | 85 | 95 | 90 |
| 说课 | 90 | 80 | 85 |
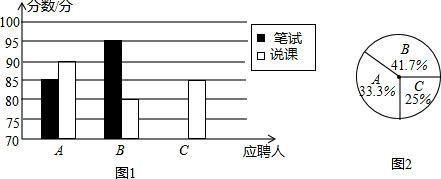
分析 (1)根据条形统计图找出A的说课成绩,填写表格即可;找出C的笔试成绩,补全条形统计图即可;
(2)由24分别乘以扇形统计图中各学生的百分数即可得到各自的得分;
(3)分别求出三位应聘人的成绩,判断即可.
解答 解:(1)由条形统计图得:A同学的说课成绩为90.填表如下:
| A | B | C | |
| 笔试 | 85 | 95 | 90 |
| 说课 | 90 | 80 | 85 |

点评 本题考查的是条形统计图与扇形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.也考查了加权平均数.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 存款额x(万元) | 划记 | 户数 |
| 1.0≤x<2.0 | 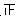 | 4 |
| 2.0≤x<3.0 | 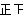 | 8 |
| 3.0≤x<4.0 | 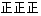 | 15 |
| 4.0≤x<5.0 | 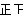 | 8 |
| 5.0≤x<6.0 | 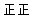 | 10 |
| 6.0≤x<7.0 | 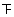 | 3 |
| 7.0≤x<8.0 | 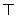 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
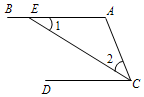 请将下列证明过程补充完整:
请将下列证明过程补充完整:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
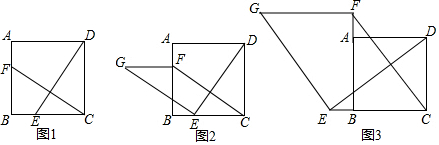
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com