
分析 先把分母因式分解和把除法运算化为乘法运算,再利用乘法的分配律计算,约分得到原式=x2+9,所以x=-$\sqrt{2015}$和x=$\sqrt{2015}$时,原式的值都为2024.
解答 解:($\frac{x-3}{x+3}$+$\frac{6x}{{x}^{2}-9}$)÷$\frac{1}{{x}^{2}-9}$=[$\frac{x-3}{x+3}$+$\frac{6x}{(x+3)(x-3)}$]•(x+3)(x-3)
=$\frac{x-3}{x+3}$•(x+3)(x-3)+$\frac{6x}{(x+3)(x-3)}$•(x+3)(x-3)
=x2-6x+9+6x
=x2+9,
当x=-$\sqrt{2015}$时,原式=(-$\sqrt{2015}$)2+9=2024;
当x=$\sqrt{2015}$时,原式=($\sqrt{2015}$)2+9=2024,
所以小亮同学做题时把“x=-$\sqrt{2015}$”错抄成了“x=$\sqrt{2015}$”,他的计算结果也是正确的.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:选择题
 如图,直线m是矩形ABCD的一条对称轴,∠ADB=30°,点P是直线m上一点,且使得△PAB和△PAD均为等腰三角形,则满足条件的点P共有( )
如图,直线m是矩形ABCD的一条对称轴,∠ADB=30°,点P是直线m上一点,且使得△PAB和△PAD均为等腰三角形,则满足条件的点P共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
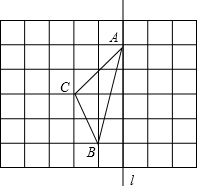 如图:在长度为1个单位的小正方形组成的网格中,点A、B、C在小正方形的顶点上.
如图:在长度为1个单位的小正方形组成的网格中,点A、B、C在小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 数 据 | 平均数 | 方差 |
| x1,x2,…,xn | $\overline{X}$ | S2 |
| x1+a,x2+a,…,xn+a | $\overline{x}$+a | S2 |
| mx1,mx2,…,mxn | m$\overline{x}$ | m2S2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com