
 x2+kx�ϣ���k��ֵ��
x2+kx�ϣ���k��ֵ��
 =3
=3
 AB=2��DG=
AB=2��DG= AD=1
AD=1
 AB=2����Q���������Ϊ2
AB=2����Q���������Ϊ2 x+4��
x+4�� ��
��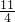 ����l��y��Ľ���Ϊ��0��
����l��y��Ľ���Ϊ��0��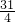 ��
��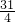
 x+4��y=-2x+
x+4��y=-2x+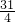 ��
�� x+4��
x+4�� ��2����
��2���� ��
�� ��2+k•
��2+k• =2��
=2��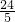
 ��32+
��32+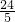 ��3=0
��3=0 x+4��
x+4�� ��2������-
��2������- ��
�� ��2+k•
��2+k• =2�����kֵ��
=2�����kֵ�� ��32+
��32+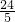 ��3=0���ó���D���������ϣ�
��3=0���ó���D���������ϣ�


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
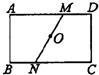
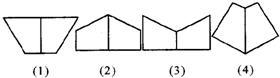
 15����ͼ��ABCD��һ�ž���ֽƬ���ع���D���ۺ۽�A�Ƿ��ۣ�ʹ�õ�A����BC�ϣ��ۺ۽�AB�ڵ�E����BC=2AB�����A��EB=
15����ͼ��ABCD��һ�ž���ֽƬ���ع���D���ۺ۽�A�Ƿ��ۣ�ʹ�õ�A����BC�ϣ��ۺ۽�AB�ڵ�E����BC=2AB�����A��EB=�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
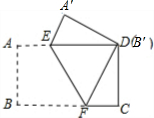 ��һ�ž���ֽƬ������ABCD������ͼ��ʽ�۵���ʹ����B�͵�D�غϣ��ۺ�ΪEF����AB=3cm��BC=5cm�����ص����֡�DEF������ǣ�������
��һ�ž���ֽƬ������ABCD������ͼ��ʽ�۵���ʹ����B�͵�D�غϣ��ۺ�ΪEF����AB=3cm��BC=5cm�����ص����֡�DEF������ǣ�������| A��7.5cm2 | B��5.1cm2 | C��5.2cm2 | D��7.2cm2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
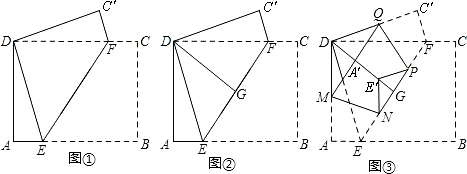
| a2+b2 |
| 3 |
| 2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com