
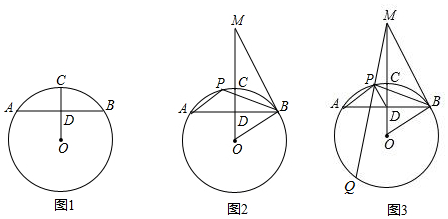
分析 (1)如图1,连接OA,利用垂径定理和圆周角定理可得结论;
(2)如图2,延长BO交⊙O于点T,连接PT,由圆周角定理可得∠BPT=90°,易得∠APT=∠APB-∠BPT=∠APB-90°,利用切线的性质定理和垂径定理可得∠ABO=∠OMB,等量代换可得∠ABO=∠APT,易得结论;
(3)如图3,连接MA,利用垂直平分线的性质可得MA=MB,易得∠MAB=∠MBA,作∠PMG=∠AMB,在射线MG上截取MN=MP,连接PN,BN,易得△APM≌△BNM,由全等三角形的性质可得AP=BN,∠MAP=∠MBN,延长PD至点K,使DK=DP,连接AK、BK,易得四边形APBK是平行四边形,由平行四边形的性质和平行线的性质可得∠PAB=∠ABK,∠APB+∠PBK=180°,由(2)得∠APB-(90°-∠MBA)=90°,易得∠NBP=∠KBP,可得△PBN≌△PBK,PN=2PH,利用三角函数的定义可得sin∠PMH=$\frac{PH}{PM}$,sin∠ABO=$\frac{3}{5}$,设DP=3a,则PM=5a,可得结果.
解答 (1)证明:如图1,连接OA,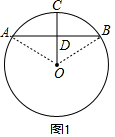
∵C是$\widehat{AB}$的中点,
∴$\widehat{AC}=\widehat{BC}$,
∴∠AOC=∠BOC,
∵OA=OB,
∴OD⊥AB,AD=BD;
(2)证明:如图2,延长BO交⊙O于点T,连接PT
∵BT是⊙O的直径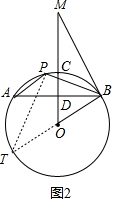
∴∠BPT=90°,
∴∠APT=∠APB-∠BPT=∠APB-90°,
∵BM是⊙O的切线,
∴OB⊥BM,
又∠OBA+∠MBA=90°,
∴∠ABO=∠OMB
又∠ABO=∠APT
∴∠APB-90°=∠OMB,
∴∠APB-∠OMB=90°;
(3)解:如图3,连接MA,
∵MO垂直平分AB,
∴MA=MB,
∴∠MAB=∠MBA,
作∠PMG=∠AMB,
在射线MG上截取MN=MP,
连接PN,BN,
则∠AMP=∠BMN,
∴△APM≌△BNM,
∴AP=BN,∠MAP=∠MBN,
延长PD至点K,
使DK=DP,
连接AK、BK,
∴四边形APBK是平行四边形;
AP∥BK,
∴∠PAB=∠ABK,∠APB+∠PBK=180°,
由(2)得∠APB-(90°-∠MBA)
=90°,
∴∠APB+∠MBA=180°
∴∠PBK=∠MBA,
∴∠MBP=∠ABK=∠PAB,
∴∠MAP=∠PBA=∠MBN,
∴∠NBP=∠KBP,
∵PB=PB,
∴△PBN≌△PBK,
∴PN=PK=2PD,
过点M作MH⊥PN于点H,
∴PN=2PH,
∴PH=DP,∠PMH=∠ABO,
∵sin∠PMH=$\frac{PH}{PM}$,sin∠ABO=$\frac{3}{5}$,
∴$\frac{PH}{PM}=\frac{3}{5}$,
∴$\frac{DP}{PM}=\frac{3}{5}$,设DP=3a,则PM=5a,
∴MQ=6DP=18a,
∴$\frac{PM}{MQ}=\frac{5}{18}$.
点评 本题主要考查了垂径定理,圆周角定理,全等三角形的判定与性质定理,三角函数的定义等相关知识,作出恰当的辅助线构建全等三角形是解答此题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{4}$=±2 | B. | ${(-\frac{1}{4})^{-2}}$=-16 | C. | x6÷x3=x2 | D. | (2x2)3=8x6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
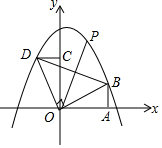 如图,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到Rt△COD,抛物线y=-$\frac{5}{6}$x2+bx+c经过B、D两点.
如图,Rt△AOB的直角边OA在x轴上,OA=2,AB=1,将Rt△AOB绕点O逆时针旋转90°得到Rt△COD,抛物线y=-$\frac{5}{6}$x2+bx+c经过B、D两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x}{(x-1)^{2}}$ | B. | $\frac{1}{x-1}$ | C. | $\frac{3}{x-1}$ | D. | $\frac{3}{x+1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com