

���� ��1����A��m��0����B��-3m��0�������뺯������ʽ�����m��ֵ���Ӷ����A��B��������꣬ȷ�������Ľ���ʽ��
��2����l����ʽ��y=-x+k�������������й�����õ�-x+k=-x2+2x+3����x2-3x+k-3=0��Ȼ�����l������������ʱ����������ֻ��һ�����㣬�õ���=21-4k=0�����kֵ����õ�P�����ꣻ
��3������M��0��m��������M��ֱ��y=kx+m���ɵã�kx+m=-x2+2x+3��Ȼ����k��ʾ��m=3k���õ���=k2-16k+16�ɵõ�3$\sqrt{{k}^{2}-16k+16}$=8-k���Ӷ����kֵ�ɵõ���M�����꣮
��� �⣺ ��1����A��m��0����B��-3m��0����
��1����A��m��0����B��-3m��0����
��$\left\{\begin{array}{l}{a{m}^{2}-2am+3=0}\\{9a{m}^{2}+6am+3=0}\end{array}\right.$��
��ã�m=-1����m=0����ȥ����
��A��-1��0����B��3��0����
��y=-x2+2x+3=-��x-1��2+4��
��2�����ڣ���ͼ��lΪֱ��BC��ƽ���ߣ�
��l������������ʱ��S��BCP�����P��QΪ�������ϵ�������ͬ�㣬
��S��BCP��S��BCQ�������
��l����ʽ��y=-x+k��
��-x+k=-x2+2x+3����x2-3x+k-3=0��
l������������ʱ����������ֻ��һ�����㣬
���=21-4k=0��
��ã�k=$\frac{21}{4}$����ʱ��x=$\frac{3}{2}$��
��P��$\frac{3}{2}$��$\frac{15}{4}$����
��3������M��0��m��������M��ֱ��y=kx+m��
�ɵã�kx+m=-x2+2x+3��
��ã�x=$\frac{2-k��\sqrt{��k-2��^{2}-4��m-3��}}{2}$��
��E��$\frac{2-k-\sqrt{��}}{2}$��$\frac{2k-{k}^{2}+k\sqrt{��}}{2}+m$����
F��$\frac{2-k+\sqrt{��}}{2}$��$\frac{2k-{k}^{2}+\sqrt{��}}{2}+m$����
�ߡ�AEO�ס�DFB��
��$\frac{AP}{DQ}=\frac{EP}{FQ}=\frac{AO}{DO}=\frac{1}{2}$��
��$\left\{\begin{array}{l}{\frac{2-k+\sqrt{��}}{2}+1=\frac{1}{2}��\frac{2-k+\sqrt{��}}{2}-1��}\\{\frac{2k-{k}^{2}-k\sqrt{��}}{2}+m=\frac{1}{2}��\frac{2k-{k}^{2}+k\sqrt{��}}{2}+m��}\end{array}\right.$
�����ã�$\left\{\begin{array}{l}{k+3\sqrt{��}=8}\\{{k}^{2}+3k\sqrt{��}-2k-2m=0}\end{array}\right.$��
��ã�m=3k��
���=k2-16k+16��
��3$\sqrt{{k}^{2}-16k+16}$=8-k��
��ã�k=8��3$\sqrt{6}$��
��m=24-9$\sqrt{6}$��m=24+9$\sqrt{6}$����ȥ����
��M��0��24-9$\sqrt{6}$����
���� �����Ƕ��κ������ۺ����ͣ������漰����֪ʶ���������ߵĶ��㹫ʽ�������ε�����������йض�������ʱҪע����������������۽����


 �ŵ������ϵ�д�
�ŵ������ϵ�д� 53������ϵ�д�
53������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | ��λ�� | C�� | ���� | D�� | ���϶����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
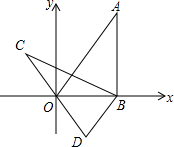 ��ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=$\sqrt{3}$x������A����AB��x���ڵ�B������ABO�Ƶ�B��ʱ����ת60��õ���CBD������B������Ϊ��2��0�������C������Ϊ��������
��ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=$\sqrt{3}$x������A����AB��x���ڵ�B������ABO�Ƶ�B��ʱ����ת60��õ���CBD������B������Ϊ��2��0�������C������Ϊ��������| A�� | ��-1��$\sqrt{3}$�� | B�� | ��-2��$\sqrt{3}$�� | C�� | ��-$\sqrt{3}$��1�� | D�� | ��-$\sqrt{3}$��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڵ�����ABC�У�AB=AC=4cm����B=30�㣬��P�ӵ�B��������$\sqrt{3}$cm/s���ٶ���BC�����˶�����Cֹͣ��ͬʱ��Q�ӵ�B��������1cm/s���ٶ���BA-AC�����˶�����Cֹͣ������BPQ�����Ϊy��cm2�����˶�ʱ��Ϊx��s�������������ܷ�ӳy��x֮�亯����ϵ��ͼ���ǣ�������
��ͼ���ڵ�����ABC�У�AB=AC=4cm����B=30�㣬��P�ӵ�B��������$\sqrt{3}$cm/s���ٶ���BC�����˶�����Cֹͣ��ͬʱ��Q�ӵ�B��������1cm/s���ٶ���BA-AC�����˶�����Cֹͣ������BPQ�����Ϊy��cm2�����˶�ʱ��Ϊx��s�������������ܷ�ӳy��x֮�亯����ϵ��ͼ���ǣ�������| A�� | 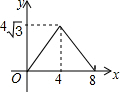 | B�� |  | C�� | 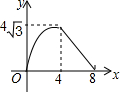 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
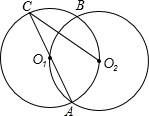 ��ͼ����Բ��O1�͡�O2�ཻ��A��B���㣬��O1������O2��Բ��O2������AO1�����ӳ�����O1�ڵ�C�����ACO2�Ķ���Ϊ��������
��ͼ����Բ��O1�͡�O2�ཻ��A��B���㣬��O1������O2��Բ��O2������AO1�����ӳ�����O1�ڵ�C�����ACO2�Ķ���Ϊ��������| A�� | 60�� | B�� | 45�� | C�� | 30�� | D�� | 20�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABCD�У���MΪDA�ӳ�����һ�㣬����BM������C��CN��BM����AD�ڵ�N����CD�ӳ�����ȡһ��F��ʹBM=CF-DN������BF����CN�ڵ�E��
��ͼ��������ABCD�У���MΪDA�ӳ�����һ�㣬����BM������C��CN��BM����AD�ڵ�N����CD�ӳ�����ȡһ��F��ʹBM=CF-DN������BF����CN�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
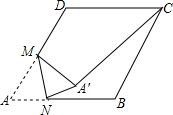 ��ͼ���ڱ߳�Ϊ2������ABCD�У���A=60�㣬��M��AD�ߵ��е㣬��N��AB����һ���㣬����AMN��MN���ڵ�ֱ�߷��۵õ���A��MN������A��C����A��C���ȵ���Сֵ�ǣ�������
��ͼ���ڱ߳�Ϊ2������ABCD�У���A=60�㣬��M��AD�ߵ��е㣬��N��AB����һ���㣬����AMN��MN���ڵ�ֱ�߷��۵õ���A��MN������A��C����A��C���ȵ���Сֵ�ǣ�������| A�� | $\sqrt{7}$ | B�� | $\sqrt{7}-1$ | C�� | $\sqrt{3}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com