
某商店将进价为每件80元的某种商品按每件100元出售,每天可售出100件.经过市场调查,发现这种商品每件每降低1元,其销售量就可增加10件.
(1)设每件商品降低售价 元,则降价后每件利润???????? 元,每天可售出???????? 件(用含
元,则降价后每件利润???????? 元,每天可售出???????? 件(用含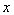 的代数式表示);
的代数式表示);
(2)如果商店为了每天获得利润2160元,那么每件商品应降价多少元?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com