从矩形的一个顶点作一条对角线的垂线,这条垂线分这条对角线成1:3两部分,则矩形的两条对角线夹角为 .
【答案】
分析:根据矩形的性质推出OA=OB,根据已知得出BE=OE,推出OA=AB,得出等边三角形AOB即可.
解答:解:
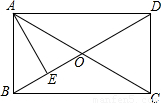
∵矩形ABCD,
∴AO=OC,OD=OB,AC=BD,
∴OA=OB=OC=OD,
∵AE⊥BD,BE:DE=1:3,
∴OE=BE,
∴AB=OA=OB,
∴△ABO是等边三角形,
∴∠AOB=60°,
∴∠AOD=180°-60°=120°,
即矩形的两条对角线夹角为60°或120°,
故答案为:60°或120°.
点评:本题考查等边三角形的性质与运用,其三边相等,三个内角相等,均为60度.
