
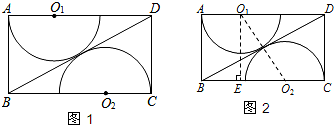 ���⣺��ͼ1��Ҫ��һ������ľ��ABCD���иƴ�ӳ�һ��Բ�����棬���ڸ�ľ�����и���뾶��ȵİ�Բ��O1�Ͱ�Բ��O2������O1��O2�ֱ���AD��BC�ϵĵ㣬��ԲO1�ֱ���AB��BD ���У���ԲO2�ֱ���CD��BD���У���AB=am��BC=bm��������ƴ�ӳɵ�Բ������İ뾶���ú�a��b�Ĵ���ʽ��ʾ����
���⣺��ͼ1��Ҫ��һ������ľ��ABCD���иƴ�ӳ�һ��Բ�����棬���ڸ�ľ�����и���뾶��ȵİ�Բ��O1�Ͱ�Բ��O2������O1��O2�ֱ���AD��BC�ϵĵ㣬��ԲO1�ֱ���AB��BD ���У���ԲO2�ֱ���CD��BD���У���AB=am��BC=bm��������ƴ�ӳɵ�Բ������İ뾶���ú�a��b�Ĵ���ʽ��ʾ����| a2+b2 |
| 4b |
| a2+b2 |
| 4b |
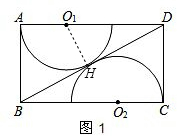 �⣺��1�����ԲO1��BD�����ڵ�H������O1H����ͼ��
�⣺��1�����ԲO1��BD�����ڵ�H������O1H����ͼ��| AB2+AD2 |
| a2+b2 |
| O1H |
| AB |
| O1D |
| BD |
| a2+b2 |
a
| ||
| b |
a
| ||
| b |
| a2+b2 |
| 4b |
a
| ||
| b |
| a2+b2 |
| a2+b2 |
| a2+b2 |
| a2+b2 |
| a2+b2 |
| 3 |
| 3 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| ���� | һ | �� | �� | �� | �� |
| ÿ���ǵ� | -0.1 | +0.25 | -0.5 | +0.4 | +0.3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
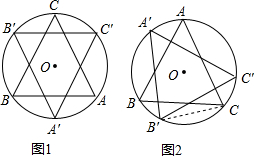 ��ͼ���߳�Ϊ2�ĵȱ�������ABC�ڽ��ڡ�O������ABC��Բ��O��˳ʱ�뷽����ת�õ���A��B��C�䣬A��C��ֱ���AB��AC����E��D���㣬����ת��Ϊ����0�㣼����360�㣩��
��ͼ���߳�Ϊ2�ĵȱ�������ABC�ڽ��ڡ�O������ABC��Բ��O��˳ʱ�뷽����ת�õ���A��B��C�䣬A��C��ֱ���AB��AC����E��D���㣬����ת��Ϊ����0�㣼����360�㣩���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ�ڡ�ABC�У���BAC=90�㣬AB=AC��CD��BA����P��BC��һ�㣬����AP������P��PE��AP��CD��E��̽��PE��PA��������ϵ��
��ͼ�ڡ�ABC�У���BAC=90�㣬AB=AC��CD��BA����P��BC��һ�㣬����AP������P��PE��AP��CD��E��̽��PE��PA��������ϵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
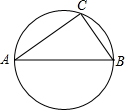 ��ͼ����O�������25�У���ABC�ڽ��ڡ�O��a��b��c�ֱ��ǡ�ABC�ġ�A����B����C�ĶԱߣ�a��b������a2+b2=c2��sinA��sinB�ֱ��ǹ���x�ķ��̣�m+5��x2-��2m-5��x+m-8=0��������
��ͼ����O�������25�У���ABC�ڽ��ڡ�O��a��b��c�ֱ��ǡ�ABC�ġ�A����B����C�ĶԱߣ�a��b������a2+b2=c2��sinA��sinB�ֱ��ǹ���x�ķ��̣�m+5��x2-��2m-5��x+m-8=0���������鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com