
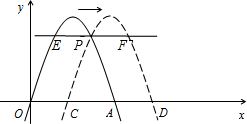
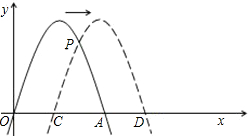
 右平移m(m>0)位,所得抛物线与x轴交于C、D点,与原抛物线交于点P
右平移m(m>0)位,所得抛物线与x轴交于C、D点,与原抛物线交于点P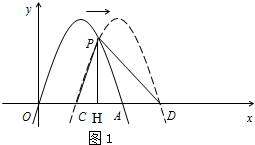 解:(1)原抛物线:y=-2x2+4x=-2(x-1)2+2,
解:(1)原抛物线:y=-2x2+4x=-2(x-1)2+2,
|
|
| m+2 |
| 2 |
| -m2+4 |
| 2 |
| m+2 |
| 2 |
| -m2+4 |
| 2 |
| -m2+4 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| m+2 |
| 2 |
| -m2+4 |
| 2 |
| -m2+4 |
| 2 |
| m2-4 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| m2-4 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| m+2 |
| 2 |
| -m2+4 |
| 2 |
| m |
| 2 |
| -m2+4 |
| 2 |
| m |
| 2 |
| m |
| 2 |
| -m2+4 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 们的长度(可用含m的式子表示);若不存在,请说明理由;
们的长度(可用含m的式子表示);若不存在,请说明理由;查看答案和解析>>
科目:初中数学 来源:2010-2011学年北京市密云县九年级(上)期末数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第20章《二次函数和反比例函数》中考题集(28):20.5 二次函数的一些应用(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年江西省中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com