
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,过抛物线的顶点
,过抛物线的顶点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为点
,垂足为点![]() ,作直线
,作直线![]() .
.
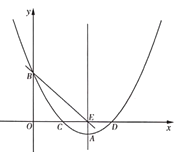
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 为第一象限内直线
为第一象限内直线![]() 上的一点,连接
上的一点,连接![]() ,取
,取![]() 的中点
的中点![]() ,作射线
,作射线![]() 交抛物线于点
交抛物线于点![]() ,设线段
,设线段![]() 的长为
的长为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 之间的函数关系式(不要求写出自变量
之间的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,在线段![]() 上有一点
上有一点![]() ,连接
,连接![]() ,
,![]() ,线段
,线段![]() 交线段
交线段![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)直线![]() 的解析式为
的解析式为![]() .(2)
.(2)![]() .(3)
.(3)![]() 或
或![]()
【解析】
(1)根据抛物线可得对称轴,可知点E的坐标,利用待定系数法可得一次函数BE的解析式;
(2)如图,作辅助线,构建直角三角形,根据抛物线过点![]() ,可得a的值,计算y=0时,x的值可得C和D两点的坐标,从而知CD的值,根据P的横坐标可表示其纵坐标,根据
,可得a的值,计算y=0时,x的值可得C和D两点的坐标,从而知CD的值,根据P的横坐标可表示其纵坐标,根据 ,
, ,列方程为
,列方程为![]() ,可得结论;
,可得结论;
(3)如图,延长HF交x轴于T,先根据已知得∠FDO=∠FTO,由等角的三角函数相等和(2)中的结论得:tan∠FDO=tan∠FTO,则![]() ,可得ET和CT的长,令∠FDO=∠FTO=2α,表示角可得∠TCQ=∠TQC,则TQ=CT=5,
,可得ET和CT的长,令∠FDO=∠FTO=2α,表示角可得∠TCQ=∠TQC,则TQ=CT=5,
设Q的坐标为![]() ,根据定理列方程可得:TS2+QS2=TQ2,
,根据定理列方程可得:TS2+QS2=TQ2,![]() ,解得
,解得![]() ,
,![]() ;根据两个t的值分别求n的值即可.
;根据两个t的值分别求n的值即可.
解:(1)抛物线的对称轴为![]() ,
,
∴![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
则 ,解得:
,解得: ,
,
∴直线![]() 的解析式为
的解析式为![]() ;
;
(2)如图,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
∵抛物线![]() 经过
经过![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,![]() .
.
∵点![]() 在抛物线
在抛物线![]() 上,∴点
上,∴点![]() 的纵坐标为
的纵坐标为![]() ,
,
∴![]() ,
,![]() ,
,
∴ ,
,
∵![]() 轴,∴
轴,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
∴![]() ,
,![]() ,在
,在![]() 中,
中, .
.
∴![]() ,
,
∴![]() .
.

(3)如图,延长![]() 交
交![]() 轴于点
轴于点![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
在![]() 中,
中,![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() ,令
,令![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵点![]() 在直线
在直线![]() 上,∴可设
上,∴可设![]() 的坐标为
的坐标为![]() .
.
过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,∴
,∴![]() ,
,
解得![]() ,
,![]() .
.
①如图2,当![]() 时,
时,![]() ,
,![]() ,
,
在![]() 中,
中, ,∴
,∴![]() ,∴
,∴![]() .
.
∴![]() .
.
②如图3,当![]() 时,
时,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() .
.



科目:初中数学 来源: 题型:
【题目】我们县是紫菜生产大县,某景点商户向游客推销一种加工好的优质紫菜,已知每千克成本为20元.市场调查发现,在一段时间内,该产品销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)的变化而变化有如下关系式:
(元/千克)的变化而变化有如下关系式:![]() .设这种紫菜在这段时间内的销售利润为
.设这种紫菜在这段时间内的销售利润为![]() (元).
(元).
(1)求![]() 与
与![]() 的关系式;
的关系式;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定该景区这种紫菜的销售单价不得高于28元/千克,该商户每天能否获得比150元更大的利润?如果能请求出最大利润,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形AOBC中,OB=4,OA=3.分别以OB,OA所在直线为x轴,y轴,建立如图1所示的平面直角坐标系.F是BC边上一个动点(不与B,C重合),过点F的反比例函数y=![]() (k>0)的图象与边AC交于点E.
(k>0)的图象与边AC交于点E.
(1)当点F运动到边BC的中点时,求点E的坐标;
(2)连接EF,求∠EFC的正切值;
(3)如图2,将△CEF沿EF折叠,点C恰好落在边OB上的点G处,求此时反比例函数的解析式.
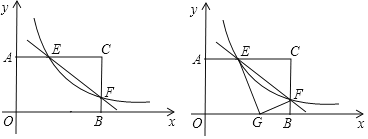
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了掌握某次数学模拟考试卷的命题质量与难度系数,命题教师选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩分为5组:第一组75~90;第二组90~105;第三组105~120;第四组120~135;第五组135~150.统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.观察图形的信息,回答下列问题:

请将频数分布直方图补充完整;若老师找到第五组中一个学生的语文、数学、英语三科成绩,如表.老师将语文、数学、英语成绩按照3:5:2的比例给出这位同学的综合分数.求此同学的综合分数.
科目 | 语文 | 数学 | 英语 |
得分 | 120 | 146 | 140 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用数学语言可表述为:“如图,CD为⊙O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,求直径CD的长”.(1尺=10寸)则CD=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com