
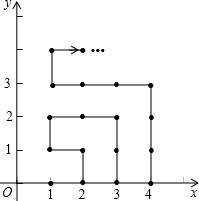
 在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中→方向排列,如(1,0),(2,0),(2,1),(1,1)(1,2),(2,2)…那么第23个点是多少?
在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中→方向排列,如(1,0),(2,0),(2,1),(1,1)(1,2),(2,2)…那么第23个点是多少? 分析 观察图形可知,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,并且右下角的点的横坐标是奇数时最后以横坐标为该数,纵坐标为0结束,当右下角的点横坐标是偶数时,以横坐标为1,纵坐标为右下角横坐标的偶数减1的点结束,根据此规律解答即可.
解答 解:根据图形,以最外边的矩形边长上的点为准,点的总个数等于x轴上右下角的点的横坐标的平方,
例如:右下角的点的横坐标为1,共有1个,1=12,
右下角的点的横坐标为2时,共有4个,4=22,
右下角的点的横坐标为3时,共有9个,9=32,
右下角的点的横坐标为4时,共有16个,16=42,
…
右下角的点的横坐标为n时,共有n2个,
∵52=25,5是奇数,25-23=2
∴第23个点是(5,2).
点评 本题考查了点的坐标的规律变化,从正方形的观点考虑求解更简便,要注意正方形的右边的点的横坐标是奇数和偶数时的不同.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
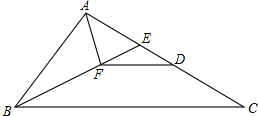 推理填空:完成下列证明:如图,E在△ABC的边AC上,且∠ABF=∠C,AF平分∠BAE交BE于点F,FD∥BC交AC于D.求证:AC-AB=DC.
推理填空:完成下列证明:如图,E在△ABC的边AC上,且∠ABF=∠C,AF平分∠BAE交BE于点F,FD∥BC交AC于D.求证:AC-AB=DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
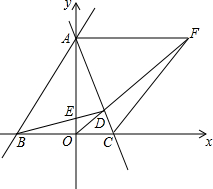 如图,在平面直角坐标系中,直线AB与直线AC分别交于x轴,y轴于点B、C、A,过点B作BD⊥AC于D,交y轴与点E,若∠BAC=45°,点B、C、E的坐标分别B(-3,0)、C(2,0)、E(0,1),过点A作AF∥x轴,交OD的延长线于点F,连接CF,在平面直角坐标系中,是否存在点K,使△OKF与△OCF全等?若存在,求出点K的坐标并画出图形;若不存在,说明理由.
如图,在平面直角坐标系中,直线AB与直线AC分别交于x轴,y轴于点B、C、A,过点B作BD⊥AC于D,交y轴与点E,若∠BAC=45°,点B、C、E的坐标分别B(-3,0)、C(2,0)、E(0,1),过点A作AF∥x轴,交OD的延长线于点F,连接CF,在平面直角坐标系中,是否存在点K,使△OKF与△OCF全等?若存在,求出点K的坐标并画出图形;若不存在,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com