
分析 (1)根据题意可以得到相应的方程,从而可以解答本题;
(2)根据题意可以得到总费用与椅子的函数关系式,再根据椅子的数量不多于课桌数量的2倍可以求得椅子的取值范围,从而可以求得最省钱的购买方案和最省总费用.
解答 解:(1)设一把椅子的售价是x元,
5×3x+5x=1000,
解得,x=50,
∴3x=150,
即一张课桌的售价是150元,一把椅子的售价是50元;
(2)设购进椅子m把,总费用为w元,
w=50m+150(500-m)=75000-100m,
∵m≤2(500-m),
解得,m≤333$\frac{1}{3}$,
∵m是整数,
∴当m=333时,w取得最小值,此时w=41700,
∴500-m=500-333=167,
即当购买333把椅子和167张桌子时最省钱,最省总费用是41700元.
点评 本题考查一次函数的应用、一元一次不等式的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函数的性质和不等式的性质解答.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:填空题
 如图,△ABC中,AB=12,AC=8,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为2.
如图,△ABC中,AB=12,AC=8,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
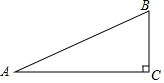 如图,在△ABC中,∠C=90°,BC=5,AB=13,则sinB是( )
如图,在△ABC中,∠C=90°,BC=5,AB=13,则sinB是( )| A. | $\frac{5}{13}$ | B. | $\frac{5}{12}$ | C. | $\frac{12}{13}$ | D. | $\frac{13}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+$\frac{1}{{x}^{2}}$=0 | B. | x3+x-1=0 | C. | x2-2xy+y2=0 | D. | x2+2x-3=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
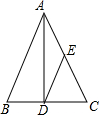 如图,△ABC中,AB=AC=15,AD平分∠BAC,点E为AC的中点,连接DE,若△CDE的周长为21,则BC的长为( )
如图,△ABC中,AB=AC=15,AD平分∠BAC,点E为AC的中点,连接DE,若△CDE的周长为21,则BC的长为( )| A. | 16 | B. | 14 | C. | 12 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com