

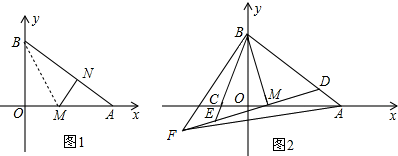
���� ��1������|a-4|+��b-3��2=0�����a��b��ֵ���ٸ���AO��BO�ij�����á�AOB�������
��2������OM=MN=x���ٸ��ݡ�ABM�����=$\frac{1}{2}$��AM��BO=$\frac{1}{2}$��AB��NM���г�����x�ķ��̣����x��ֵ��������OM�ij�д����M�����ꣻ
��3���ȸ�����֪�����ó���BED=��BDE���ٸ���������ʣ�����BEDת��Ϊ��FBE+��BFE����BDEת��Ϊ��BAF+��AFD�������ݵ�ʽ���ʣ�����FBE+��BFE=��BAF+��AFD���б��Σ����ɵó����ۣ�
��� �⣺��1����ͼ1����A��a��0����B��0��b����a��b����|a-4|+��b-3��2=0��
�����$\left\{\begin{array}{l}{a-4=0}\\{b-3=0}\end{array}\right.$���ɵ�$\left\{\begin{array}{l}{a=4}\\{b=3}\end{array}\right.$��
��A��4��0����B��0��3����
��AO=4��BO=3��
���ABO�����=$\frac{1}{2}$��AO��BO=$\frac{1}{2}$��4��3=6��
��2����ͼ1�����۵��ɵã���BNM=��AOB=90�㣬MO=NM��
��OM=MN=x����AM=4-x��
�ߡ�ABM�����=$\frac{1}{2}$��AM��BO=$\frac{1}{2}$��AB��NM��
��$\frac{1}{2}$����4-x����3=$\frac{1}{2}$��5��x��
���x=$\frac{3}{2}$��
��OM=$\frac{3}{2}$��
���M��������$\frac{3}{2}$��0����
��3����FBE���AFD֮�����������ϵ����FBE=2��AFD��
�������£�
��ͼ2����BMƽ�֡�CBA��DE��BM��
���BED=��BDE��
�֡ߡ�BED=��FBE+��BFE����BDE=��BAF+��AFD��
���FBE+��BFE=��BAF+��AFD��
�֡ߡ�BFE=��BFA-��AFD��
���FBE+����BFA-��AFD��=��BAF+��AFD��
�൱��BFA=��BAFʱ����FBE-��AFD=��AFD��
����FBE=2��AFD��
���� �����Է��ۣ���Գƣ��任Ϊ��������Ҫ�����������ε���������Լ���ǵ����ʣ��ڣ�2����Ҳ���Ը���ֱ��������AMN�еĹ��ɶ������г�����x�ķ��̽�����⣮��ڣ�3����Ĺؼ���������ǵ����ʣ���������ȵĽǶ�����ת����


 ��ĩ�óɼ�ϵ�д�
��ĩ�óɼ�ϵ�д� 99��1������ĩ��ѵ��ϵ�д�
99��1������ĩ��ѵ��ϵ�д� ��ǿ��У��ĩ���100��ϵ�д�
��ǿ��У��ĩ���100��ϵ�д� �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д� ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ���䣨�꣩ | 12 | 13 | 14 | 15 | 16 |
| ���� | 1 | 2 | 7 | 6 | 2 |
| A�� | 13�� | B�� | 14�� | C�� | 15�� | D�� | 16�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ���л�������λ������ | 7 | 8 | 9 | 10 |
| ��������Ӧ�����Ĵ��� | 2 | 2 | 0 | 1 |
| ��������Ӧ�����Ĵ��� | 1 | 3 | 1 | 0 |
| A�� | 5��5 | B�� | 40��40 | C�� | 8��8 | D�� | 25��24 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��$\frac{1}{2}$ | B�� | x��$\frac{1}{2}$ | C�� | x��-2 | D�� | x=$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | 7 | C�� | 8 | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -xy2 | B�� | 5xy2 | C�� | -x2y4 | D�� | 5x2y4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com