
分析 (1)根据下载速度不变,将开始时下载甲、乙文件的速度相加即可得出结论;
(2)设后来下载甲的度数为xMB/s,时间为ys,则后来下载乙的速度为(24-x)MB/s,根据总下载甲文件的时间为30s结合题意即可得出关于x、y的二元二次方程组,解方程组即可得出结论.
解答 解:(1)这次下载的总速度为:15+9=24MB/s.
(2)设后来下载甲的度数为xMB/s,时间为ys,则后来下载乙的速度为(24-x)MB/s,
根据题意,得:$\left\{\begin{array}{l}{(24-x)•y-xy=160}\\{9×(30-y)+(24-x)•y=410}\end{array}\right.$,
整理,得:$\left\{\begin{array}{l}{12-xy=80}\\{15y-xy=140}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=8}\\{y=20}\end{array}\right.$.
答:后来下载甲文件的速度为8MB/s,下载时间为20s.
点评 本题考查了二元二次方程组的应用,根据数量关系列出关于x、y的二元二次方程组是解题的关键.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.
如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
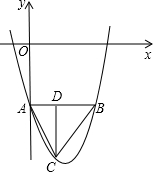 如图,已知二次函数y=ax2+bx+c的图象的顶点的坐标为(2,-9),与y轴交于点A(0,-5).
如图,已知二次函数y=ax2+bx+c的图象的顶点的坐标为(2,-9),与y轴交于点A(0,-5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
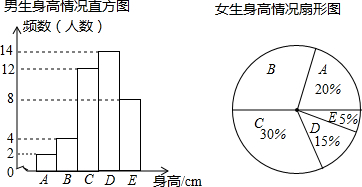 为了解我校初一年级学生的身高情况,随机对初一男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据调查所得数据绘制如图所示的统计图表.由图表中提供的信息,回答下列问题:
为了解我校初一年级学生的身高情况,随机对初一男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据调查所得数据绘制如图所示的统计图表.由图表中提供的信息,回答下列问题:| 组别 | 身高(cm) |
| A | x<150 |
| B | 150≤x<155 |
| C | 155≤x<160 |
| D | 160≤x<165 |
| E | x≥165 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com