
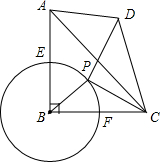
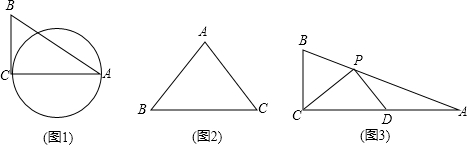
 ��ͼ���ڵ���ֱ��������ABC�У���ABC=90�㣬AB=BC=4����B��AB��BC����E��F����P�ǻ�EF�ϵ�һ�����㣬����PC���߶�PC��P����ʱ����ת90�㵽PD������CD��AD��
��ͼ���ڵ���ֱ��������ABC�У���ABC=90�㣬AB=BC=4����B��AB��BC����E��F����P�ǻ�EF�ϵ�һ�����㣬����PC���߶�PC��P����ʱ����ת90�㵽PD������CD��AD������ ��1���ɵ���ֱ�������ε����ʿ�֪��BC��AC=PC��DC����PCD=��ACB���Ӷ���֤����BCP=��ACD������������߶�Ӧ�ɱ����Ҽн���ȵ������������ƽ���֤�����ɣ�
��2����ͼ1��ʾ������á�ABC�������Ȼ��ɵõ���ADC����������������ε������ʽ�ɵõ�AD�ij���Ȼ���������������ζ�Ӧ�߳����������PB�ij���
��3����ͼ2��ʾ�������������ε����ʿ�֪��AD=2$\sqrt{2}$�����ǿɵõ���D����AΪԲ�ģ���2$\sqrt{2}$Ϊ�뾶��Բ�ϣ�Ȼ����ݵ�P��ԲB���˶�·�ߺ�ȷ����D������·�����������Ե�Բ�Ľǣ�������ݻ�����ʽ��⼴�ɣ�
��� �⣺��1���ߡ�ABC=90�㣬AB=BC��
���ACB=45�㣬BC��AC=1��$\sqrt{2}$��
��PD=PC����DPC=90�㣬
���PCD=45�㣬PC��DC=1��$\sqrt{2}$��
��BC��AC=PC��DC����PCD=��ACB��
���PCD-��PCA=��ACB-��PCA������BCP=��ACD��
���BPC�ס�ADC��
��2����ͼ1��ʾ��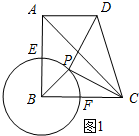
��AB=BC=4����ABC=90�㣬
��S��ABC=$\frac{1}{2}$AB•BC=$\frac{1}{2}$��4��4=8��
���ı���ABCD�����Ϊ12��
��S��ADC=4��
��AD��BC��
��S��ADC=$\frac{1}{2}$AD•AB=4����$\frac{1}{2}$��4��AD=4��
��AD=2��
�ߡ�BPC�ס�ADC��
��$\frac{AD}{BP}=\frac{AC}{BC}=\frac{\sqrt{2}}{1}$����$\frac{2}{BP}=\frac{\sqrt{2}}{1}$��
���BP=$\sqrt{2}$��
���B�İ뾶Ϊ$\sqrt{2}$��
��3����ͼ2��ʾ��
��BP=2���ɣ�2����֪AD��BP=$\sqrt{2}$��1��
��AD=2$\sqrt{2}$��
��D����AΪԲ�ģ���2$\sqrt{2}$Ϊ�뾶��Բ�ϣ�
�ߡ�BPC�ס�ADC��
���PBC=��DAC��
�ߵ���P���E�غ�ʱ����PBC=90�㣮
���DAC=90�㣮
����P��C��ԲB����ʱ����BP��C=90�㣬BP��=2��BC=4��
���P��BC=60�㣮
���D��AC=60�㣮
���D��AD=90��-60��=30�㣮
���D�˶���·�߳�=$\frac{30��2\sqrt{2}��}{180}$=$\frac{\sqrt{2}��}{3}$��
���� ������Ҫ�������Բ���ۺ�Ӧ�ã��������ҪӦ���˵���ֱ�������ε����ʡ����������ε����ʺ��ж������εĻ�����ʽ��Ӧ�ã��������������ε�����ȷ������D�˶���·������״�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -3 | B�� | -$\frac{1}{3}$ | C�� | 3 | D�� | -12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
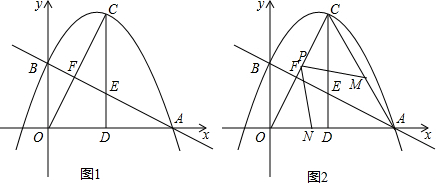
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢� | C�� | �٢ڢ� | D�� | �٢ڢۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{{\begin{array}{l}{8x-3=y}\\{7x+4=y}\end{array}}\right.$ | B�� | $\left\{{\begin{array}{l}{8x+3=y}\\{7x-4=y}\end{array}}\right.$ | C�� | $\left\{{\begin{array}{l}{y-8x=3}\\{y-7x=4}\end{array}}\right.$ | D�� | $\left\{{\begin{array}{l}{8x-y=3}\\{7x-y=4}\end{array}}\right.$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��AB�ǡ�O��ֱ����C��D�ǡ�O�ϵĵ㣬��OC��BD��AD�ֱ���BC��OC�ཻ�ڵ�E��F�������н��ۣ�
��ͼ��AB�ǡ�O��ֱ����C��D�ǡ�O�ϵĵ㣬��OC��BD��AD�ֱ���BC��OC�ཻ�ڵ�E��F�������н��ۣ�| A�� | �ڢܢݢ� | B�� | �٢ۢݢ� | C�� | �ڢۢܢ� | D�� | �٢ۢܢ� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com