
【题目】为了增强公民的节水意识,合理利用水资源,某市采用价格调控手段来引导市民节约用水:每户居民每月用水不超过15立方米时,按基本价格x元/立方米进行收费;超过15立方米时,加价收费,超过的部分按y元/立方米收费.该市某户居民今年3、4、5月份的用水量和水费如下表所示:
月份 | 用水量(立方米) | 水费(元) |
3 | 16 | 50 |
4 | 20 | 70 |
5 | m | 不低于36元且不超过95元 |
(1)求x、y的值;
(2)求该居民5月份用水量m的范围.
科目:初中数学 来源: 题型:
【题目】已知函数y=mx2+(2m+1)x+2(m为实数). 
(1)请探究该函数图象与x轴的公共点个数的情况(要求说明理由);
(2)在图中给出的平面直角坐标系中分别画出m=﹣1和m=1的函数图象,并根据图象直接写出它们的交点坐标;
(3)探究:对任意实数m,函数的图象是否一定过(2)中的点,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根,且OA>OB.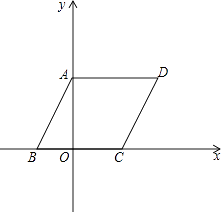
(1)求OA、OB的长.
(2)若点E为x轴正半轴上的点,且S△AOE= ![]() ,求经过D、E两点的直线解析式及经过点D的反比例函数的解析式,并判断△AOE与△AOD是否相似.
,求经过D、E两点的直线解析式及经过点D的反比例函数的解析式,并判断△AOE与△AOD是否相似.
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将n个边长都为2的正方形按如图所示摆放,点A1 , A2 , …An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( ) 
A.n
B.n﹣1
C.4(n﹣1)
D.4n
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,若点P(4,0)在该抛物线上,则一元二次方程ax2+bx+c=0的两根为 . 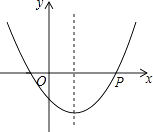
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC与△DEF中,给出以下六个条件:
(1)AB=DE;(2)BC=EF;(3)AC=DF;(4)∠A=∠D;(5)∠B=∠E;(6)∠C=∠F.
以其中三个作为已知条件,不能判断△ABC与△DEF全等的是( )

A. (1)(5)(2) B. (1)(2)(3) C. (2)(3)(4) D. (4)(6)(1)
查看答案和解析>>
科目:初中数学 来源: 题型:
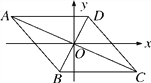
【题目】如图,已知点A(-4,2),B(-1,-2),□ABCD的对角线交于坐标原点O.
(1)请写出点C,D的坐标;
(2)指出从线段AB到线段DC的变换过程;
(3)求□ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小张某天上午营运全是在东西走向的政府大道上进行的,如果规定向东为正,向西为负,他这天上午的行程是(单位:千米):+15,-3,+16,-11,+10,-12,+4,-15,+16,-18.
(1)将最后一名乘客送达目的地时,小张距上午出发点的距离是多少千米?在出发点的什么方向?
(2)若汽车耗油量为0.6升/千米,出车时,邮箱有油72.2升,若小张将最后一名乘客送达目的地,再返回出发地,问小张今天上午是否需要加油?若要加油至少需要加多少才能返回出发地?若不用加油,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y= ![]() (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是( )
(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是( ) 
A.b=2a+k
B.a=b+k
C.a>b>0
D.a>k>0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com