
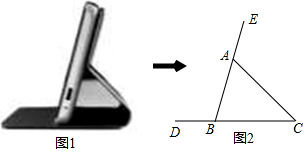
分析 作BF⊥AC于F,根据等腰三角形的性质和∠ABC=75°,求出∠ABF的度数,根据三角函数和AC=5.46cm求出BF的长,即点B到AC的距离.
解答 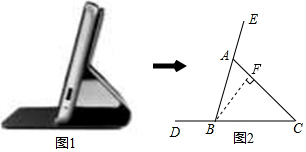 解:作BF⊥AC于F,
解:作BF⊥AC于F,
∵∠C=45°,
∴∠CBF=45°,
∴BF=CF,
∵∠ABC=75°,
∴∠ABF=30°,
∴AF=$\frac{\sqrt{3}}{3}$BF,
∵AC=5.46cm,
∴BF+$\frac{\sqrt{3}}{3}$BF=5.46,
解得BF≈3.5cm.
即点B到AC的距离大约为3.5cm.
故答案为:3.5.
点评 本题考查的是解直角三角形的应用,掌握锐角三角函数的概念是解题的关键,作出合适的辅助线构造直角三角形是解题的重要环节.


科目:初中数学 来源: 题型:解答题
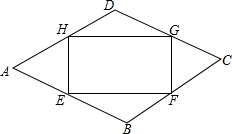 如图,某校园内有一块菱形的空地ABCD,为了美化环境,现要进行绿化,计划在中间建设一个面积为S的矩形绿地EFGH,其中,点E、F、G、H分别在菱形的四条边上,AB=a米,BE=BF=DG=DH=x米,∠A=60°
如图,某校园内有一块菱形的空地ABCD,为了美化环境,现要进行绿化,计划在中间建设一个面积为S的矩形绿地EFGH,其中,点E、F、G、H分别在菱形的四条边上,AB=a米,BE=BF=DG=DH=x米,∠A=60°查看答案和解析>>
科目:初中数学 来源: 题型:选择题
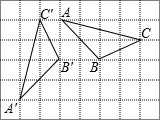 如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△A′B′C′的各个顶点均在格点处,且△A′B′C′是由△ABC以网格中的某个格点为旋转中心,逆时针旋转90°得到的,点A,B,C的对应点分别为点A′,B′,C′,则在旋转过程中,点A经过的路径长为( )
如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△A′B′C′的各个顶点均在格点处,且△A′B′C′是由△ABC以网格中的某个格点为旋转中心,逆时针旋转90°得到的,点A,B,C的对应点分别为点A′,B′,C′,则在旋转过程中,点A经过的路径长为( )| A. | $\frac{\sqrt{10}}{4}$π | B. | $\frac{\sqrt{13}}{2}$π | C. | $\frac{\sqrt{13}}{4}$π | D. | $\frac{\sqrt{10}}{2}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
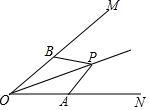 如图,点P在∠MON的平分线上,点A、B在∠MON的两边上,若要使△AOP≌△BOP,那么需要添加一个条件是AO=BO或∠OAP=∠OBP或∠APO=∠BPO(写出一个即可).
如图,点P在∠MON的平分线上,点A、B在∠MON的两边上,若要使△AOP≌△BOP,那么需要添加一个条件是AO=BO或∠OAP=∠OBP或∠APO=∠BPO(写出一个即可).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 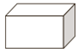 | B. | 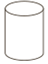 | C. | 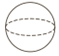 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com