
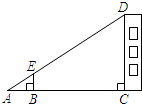
 如图,利用标杆BE测量建筑物的高度.若标杆BE的高为1.2m,测得AB=1.6m,BC=12.4m,则楼高CD为10.5m.
如图,利用标杆BE测量建筑物的高度.若标杆BE的高为1.2m,测得AB=1.6m,BC=12.4m,则楼高CD为10.5m. 分析 先证明∴△ABE∽△ACD,则利用相似三角形的性质得$\frac{1.6}{1.6+12.4}$=$\frac{1.2}{CD}$,然后利用比例性质求出CD即可.
解答 解:∵EB∥CD,
∴△ABE∽△ACD,
∴$\frac{AB}{AC}$=$\frac{BE}{CD}$,即$\frac{1.6}{1.6+12.4}$=$\frac{1.2}{CD}$,
∴CD=10.5(米).
故答案为10.5.
点评 本题考查了相似三角形的应用:借助标杆或直尺测量物体的高度.利用杆或直尺测量物体的高度就是利用杆或直尺的高(长)作为三角形的边,利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:解答题
| 里程(单位:km) | 收费(单位:元) |
| 3km以下(含3km) | 8.0 |
| 3km以上(每增加1km) | 1.80 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-2(x+2)2+3 | B. | y=-3(x-2)2+3 | C. | y=-5(x+2)2-3 | D. | y=-5(x-2)2-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
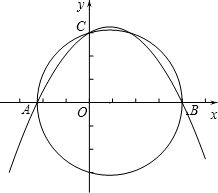 如图,在平面直角坐标系xOy中,已知点A(-$\frac{9}{4}$,0),点C(0,3),点B是x轴上一点(位于点A的右侧,以AB为直径的圆恰好经过点C)
如图,在平面直角坐标系xOy中,已知点A(-$\frac{9}{4}$,0),点C(0,3),点B是x轴上一点(位于点A的右侧,以AB为直径的圆恰好经过点C)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
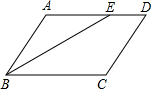 如图,在四边形ABCD中,BE平分∠ABC,∠AEB=∠ABE.
如图,在四边形ABCD中,BE平分∠ABC,∠AEB=∠ABE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
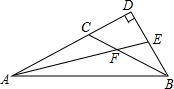 如图,在△ABC中,∠CAB=∠ABC=$\frac{1}{4}$∠ACB,AF是∠CAB的平分线,延长AF交AC边上的高BD于点E,求∠AEB的度数.
如图,在△ABC中,∠CAB=∠ABC=$\frac{1}{4}$∠ACB,AF是∠CAB的平分线,延长AF交AC边上的高BD于点E,求∠AEB的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com