
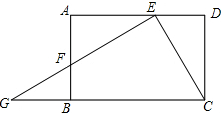
 如图,已知矩形ABCD中,E是AD上的一点,过点E作EF⊥EC交边AB于点F,交CB的延长线于点G,且EF=EC.
如图,已知矩形ABCD中,E是AD上的一点,过点E作EF⊥EC交边AB于点F,交CB的延长线于点G,且EF=EC.分析 (1)由矩形的性质得出∠A=∠D=90°,再根据角的互余关系证出∠AFE=∠DEC,根据AAS证明△AEF≌△DCE,得出对应边相等即可;
(2)设CD=AE=x,则AD=x+6,根据矩形的周长列出方程,解方程求出AE、CD,得出BF、BC,再证明△AEF∽△BGF,得出比例式求出BG,即可得出CG.
解答 (1)证明:∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠AEF+∠AFE=90°,
∵EF⊥EC,
∴∠FEC=90°,
∴∠AEF+∠DEC=90°,
∴∠AFE=∠DEC,
在△AEF和△DCE中,$\left\{\begin{array}{l}{∠A=∠D}&{\;}\\{∠AFE=∠DEC}&{\;}\\{EF=EC}&{\;}\end{array}\right.$,
∴△AEF≌△DCE(AAS),
∴CD=AE,DE=AF;
(2)解:设CD=AE=x,则AD=x+6,
∵矩形ABCD的周长为48,
∴2(x+6+x)=48,
解得:x=9,
∴AE=CD=9,AB=CD=9,AD=BC=15,
∴BF=AB-AF=3,
∵四边形ABCD是矩形,
∴AD∥BC,
∴△AEF∽△BGF,
∴$\frac{AE}{BG}=\frac{AF}{BF}$,
即$\frac{9}{BG}=\frac{6}{3}$,
∴BG=4.5,
∴CG=BC+BG=15+4.5=19.5.
点评 本题考查了矩形的性质、全等三角形的判定与性质、相似三角形的判定与性质;熟练掌握矩形的性质,并能进行推理论证与计算是解决问题的关键.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:解答题
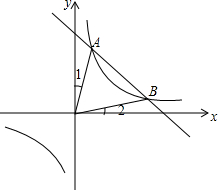 如图,函数y1=$\frac{{k}_{1}}{x}$的图象与函数y2=k2x+b的图象交于A,B两点,已知A点的坐标为(1,4).
如图,函数y1=$\frac{{k}_{1}}{x}$的图象与函数y2=k2x+b的图象交于A,B两点,已知A点的坐标为(1,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
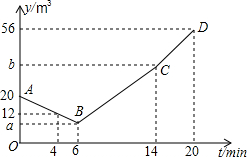 水池中有水20m3,12:00时同时打开两个每分钟出水量相等且不变的出水口,12:06时王师傅打开一个每分钟进水量不变的进水口,同时关闭一个出水口,12:14时再关闭里另一个出水口,12:20时水池中有水56cm3,王师傅的具体记录如表,设从12:00开始经过tmin池中有水ym3,如图中折线ABCD表示y关于t的函数图象.
水池中有水20m3,12:00时同时打开两个每分钟出水量相等且不变的出水口,12:06时王师傅打开一个每分钟进水量不变的进水口,同时关闭一个出水口,12:14时再关闭里另一个出水口,12:20时水池中有水56cm3,王师傅的具体记录如表,设从12:00开始经过tmin池中有水ym3,如图中折线ABCD表示y关于t的函数图象.| 时间 | 池中有水(m3) |
| 12:00 | 20 |
| 12:04 | 12 |
| 12:06 | a |
| 12:14 | b |
| 12:20 | 56 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y2<y1<y3 | D. | y3<y1<y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com