
(本小题满分14分)
已知:如图,抛物线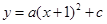 与y轴交于点C(0,
与y轴交于点C(0, ), 与x轴交于点A、 B,点A的坐标为(2,0).
), 与x轴交于点A、 B,点A的坐标为(2,0).
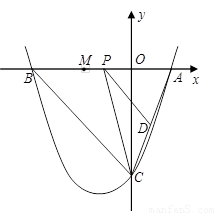
(1)求该抛物线的解析式;
(2)点P是线段AB上的动点,过点P作PD∥BC,交AC于点D,连接CP.当△CPD的面积最大时,求点P的坐标;
(3)若平行于x轴的动直线 与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(
与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(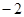 ,0).问:是否存在这样的直线
,0).问:是否存在这样的直线 ,使得△OMF是等腰三角形?若存 在,请求出点Q的坐标;若不存在,请说明理由.
,使得△OMF是等腰三角形?若存 在,请求出点Q的坐标;若不存在,请说明理由.
(1)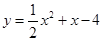
(2)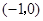
(3) 或
或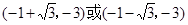
【解析】(1)由题意,得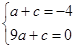
解得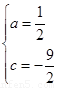 .……2分
.……2分
∴所求抛物线的解析式为: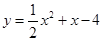 ..……3分
..……3分
(2)设点P的坐标为(x,0),过点D作DG⊥x轴于点G.
∴由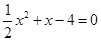 ,得
,得 .
.
∴点A的坐标为(2,0),点B的坐标为(-4,0)..……4分
∴AB=6,BP=2-x.
∵点P在线段AB上,
∴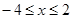 ..……5分
..……5分
∵PD∥BC,
∴△APD∽△ABC
∴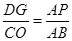
即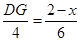 ,∴
,∴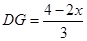 .
.
∴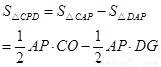
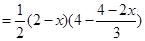
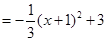 .……8分
.……8分
又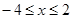 ,
,
∴当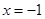 时,
时,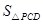 有最大值3,此时P
有最大值3,此时P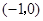 ..……9分
..……9分
(3)存在.
在△OMF中.
①若MO=MF,∵B(-4,0),M(-2,0),故BM=OM=MF=2.
又在Rt△BOC中,OB=OC=4,∴∠OBC=45°.∴∠MFB=∠OBC=45°.
∴∠BMF=90°.此时,点F的坐标为(-2,-2).
由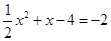 ,得
,得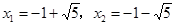 .
.
此时,点Q的坐标为: ..……11分
..……11分
②若OF=MF,过点F作FE⊥x轴于点E,
由等腰三角形的性质得: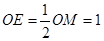 ,∴BE=3,
,∴BE=3,
∴在等腰直角△BEF中,EF=BE=3.∴F(-1,-3).
由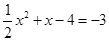 ,得
,得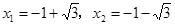 .
.
此时,点Q的坐标为: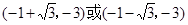 ..……13分
..……13分
③若OM=OF,∵OB=OC=4,且∠BOC=90°,∴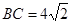 ,
,
∴点O到BC的距离为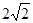 ,而OF=OM=2<
,而OF=OM=2<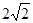 ,
,
此时,不存在这样的直线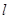 ,使得△OMF是等腰三角形..……14分
,使得△OMF是等腰三角形..……14分
综上所述,存在这样的直线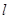 ,使得△OMF是等腰三角形.所求点Q的坐标为:
,使得△OMF是等腰三角形.所求点Q的坐标为:
 或
或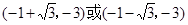 .
.


科目:初中数学 来源: 题型:
25.(本小题满分14分)
 如图13,二次函数
如图13,二次函数![]() 的图象与x轴交于A、B两点,与y轴交于点C(0,-1),ΔABC的面积为
的图象与x轴交于A、B两点,与y轴交于点C(0,-1),ΔABC的面积为![]() 。
。
(1)求该二次函数的关系式;
(2)过y轴上的一点M(0,m)作y轴上午垂线,若该垂线与ΔABC的外接圆有公共点,求m的取值范围;
(3)在该二次函数的图象上是否存在点D,使四边形ABCD为直角梯形?若存在,求出点D的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
(2011广西崇左,25,14分)(本小题满分14分)已知抛物线y=x2+4x+m(m为常数)
经过点(0,4).
(1) 求m的值;
(2) 将该抛物线先向右、再向下平移得到另一条抛物线.已知平移后的抛物线满足下述两个条件:它的对称轴(设为直线l2)与平移前的抛物线的对称轴(设为直线l1)关于y轴对称;它所对应的函数的最小值为-8.
① 试求平移后的抛物线的解析式;
② 试问在平移后的抛物线上是否存在点P,使得以3为半径的圆P既与x轴相切,又与直线l2相交?若存在,请求出点P的坐标,并求出直线l2被圆P所截得的弦AB的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
 与y轴交于点C(0,
与y轴交于点C(0, ), 与x轴交于点A、 B,点A的坐标为(2,0).
), 与x轴交于点A、 B,点A的坐标为(2,0).
 与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(
与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为( ,0).问:是否存在这样的直线
,0).问:是否存在这样的直线 ,使得△OMF是等腰三角形?若存 在,请求出点Q的坐标;若不存在,请说明理由.
,使得△OMF是等腰三角形?若存 在,请求出点Q的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2011年广东省萝岗区初中毕业班综合测试数学卷 题型:解答题
(本小题满分14分)
如图1,抛物线 与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线
与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线 与抛物线交于点B、C.
与抛物线交于点B、C.
【小题1】(1)求点A的坐标;
【小题2】(2)当b=0时(如图2),求 与
与 的面积。
的面积。
【小题3】(3)当 时,
时, 与
与 的面积大小关系如何?为什么?
的面积大小关系如何?为什么?
【小题4】(4)是否存在这样的b,使得 是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.
是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(内蒙古赤峰卷)数学 题型:解答题
(2011广西崇左,25,14分)(本小题满分14分)已知抛物线y=x2+4x+m(m为常数)
经过点(0,4).
(1) 求m的值;
(2) 将该抛物线先向右、再向下平移得到另一条抛物线.已知平移后的抛物线满足下述两个条件:它的对称轴(设为直线l2)与平移前的抛物线的对称轴(设为直线l1)关于y轴对称;它所对应的函数的最小值为-8.
① 试求平移后的抛物线的解析式;
② 试问在平移后的抛物线上是否存在点P,使得以3为半径的圆P既与x轴相切,又与直线l2相交?若存在,请求出点P的坐标,并求出直线l2被圆P所截得的弦AB的长度;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com