
如图1,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转, DE,DF分别交线段AC于点M,K.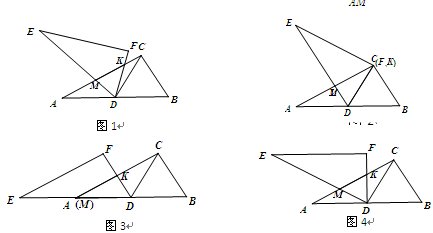
(1)观察: ①如图2、图3,当∠CDF="0°" 或60°时,AM+CK_______MK(填“>”,“<”或“=”).
②如图4,当∠CDF="30°" 时,AM+CK___MK(只填“>”或“<”).
(2)猜想:如图1,当0°<∠CDF<60°时,AM+CK_______MK,证明你所得到的结论.
(3)如果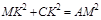 ,请直接写出∠CDF的度数和
,请直接写出∠CDF的度数和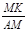 的值.
的值.
(1)①在Rt△ABC中,D是AB的中点,
∴AD=BD=CD=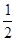 AB,∠B=∠BDC=60°
AB,∠B=∠BDC=60°
又∵∠A=30°,
∴∠ACD=60°-30°=30°,
又∵∠CDE=60°,或∠CDF=60°时,
∴∠CKD=90°,
∴在△CDA中,AM(K)=CM(K),即AM(K)=KM(C)(等腰三角形底边上的垂线与中线重合),
∵CK=0,或AM=0,
∴AM+CK=MK;………………………………………2分
②由①,得
∠ACD=30°,∠CDB=60°,
又∵∠A=30°,∠CDF=30,∠EDF=60°,
∴∠ADM=30°,
∴AM=MD,CK=KD,
∴AM+CK=MD+KD,
∴在△MKD中,AM+CK>MK(两边之和大于第三边).………………………………………2分
(2)> ………………………………………2分
证明:作点C关于FD的对称点G,
连接GK,GM,GD,
则CD=GD,GK=CK,∠GDK=∠CDK,
∵D是AB的中点,∴AD=CD=GD、
∵∠A=30°,∴∠CDA=120°,
∵∠EDF=60°,∴∠GDM+∠GDK=60°,
∠ADM+∠CDK=60°.
∴∠ADM=∠GDM,…………………………………3分
∵DM=DM,
∴AD=DG,∠ADM=∠GDM,DM=DM
∴△ADM≌△GDM,(SAS)
∴GM=AM.
∵GM+GK>MK,∴AM+CK>MK.…………………………………………1分
(3)由(2),得GM=AM,GK=CK,
∵MK2+CK2=AM2,
∴MK2+GK2=GM2,
∴∠GKM=90°,
又∵点C关于FD的对称点G,
∴∠CKG=90°,∠FKC=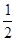 ∠CKG=45°,
∠CKG=45°,
又有(1),得∠A=∠ACD=30°,
∴∠FKC=∠CDF+∠ACD,
∴∠CDF=∠FKC-∠ACD=15°,
在Rt△GKM中,∠MGK=∠DGK+∠MGD=∠A+∠ACD=60°,
∴∠GMK=30°,
∴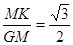 ,
,
∴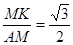 .…………………………………………2分
.…………………………………………2分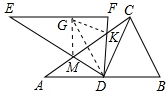
解析


科目:初中数学 来源: 题型:
 (2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论:
(2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论:
| ||
| 2 |
| AC |
| CM |
| BC |
| CA |
| CM |
| AB |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为
(2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为2
| ||
| π |
2
| ||
| π |
查看答案和解析>>
科目:初中数学 来源: 题型:
 的外接圆.
的外接圆.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•嘉定区二模)如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,且BC2=CD•CA.
(2013•嘉定区二模)如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,且BC2=CD•CA.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com