
| 3 |
| 5 |
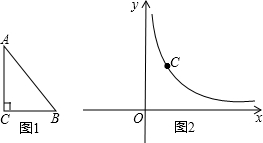 角坐标系中,使斜边AB落在x轴上,直角顶点C(1,3)落在反比例函数y=
角坐标系中,使斜边AB落在x轴上,直角顶点C(1,3)落在反比例函数y=| k |
| x |
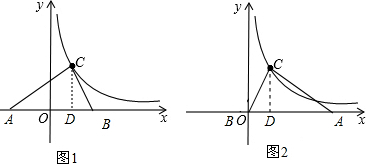 解:(1)作CD⊥x轴于D.则CD=3.
解:(1)作CD⊥x轴于D.则CD=3.| k |
| x |
| CD |
| AC |
| 3 |
| 5 |
| AC2-CD2 |


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源: 题型:
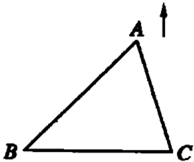 20、如图,在△ABC中,BC边不动,点A是一个动点.当点A竖直向上运动,∠A越来越小,∠B、∠C越来越大.若∠A减少α度,∠B增加β度,∠C增加γ度,请写出α、β、γ三者之间的等量关系,并说明你是如何得到的.
20、如图,在△ABC中,BC边不动,点A是一个动点.当点A竖直向上运动,∠A越来越小,∠B、∠C越来越大.若∠A减少α度,∠B增加β度,∠C增加γ度,请写出α、β、γ三者之间的等量关系,并说明你是如何得到的.查看答案和解析>>
科目:初中数学 来源: 题型:
 30、如图,在△ABC中,AB=AC,D是BC的中点,连接AD.DE⊥AB,DF⊥AC,E,F是垂足.图中共有多少对全等三角形?请直接用“≌”符号把它们分别表示出来.(不要求证明)
30、如图,在△ABC中,AB=AC,D是BC的中点,连接AD.DE⊥AB,DF⊥AC,E,F是垂足.图中共有多少对全等三角形?请直接用“≌”符号把它们分别表示出来.(不要求证明)查看答案和解析>>
科目:初中数学 来源: 题型:
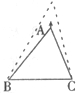 14、如图,在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大.若∠A减小x°,∠B增加y°,∠C增加z°,则x,y,z之间的关系是( )
14、如图,在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大.若∠A减小x°,∠B增加y°,∠C增加z°,则x,y,z之间的关系是( )查看答案和解析>>
科目:初中数学 来源: 题型:
 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 3 |
| 3 |
| 5 |
2-2
|
2-2
|
查看答案和解析>>
科目:初中数学 来源:2011-2012学年四川省沐川县初三二调考试数学卷(解析版) 题型:解答题
从甲、乙两题中选做一题,如果两题都做,只以甲题计分.
1.甲题:若关于x的一元二次方程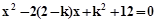 有实数根α、β.求实数k的取值范围;设
有实数根α、β.求实数k的取值范围;设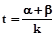 ,求t的最小值.
,求t的最小值.
2.乙题:如图,在△ABC 中,点O是AC边上的一个动点,过点O作直
线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.当点O运动到何处时,四边形AECF是矩形?并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com