
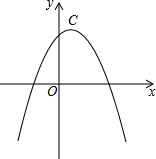
 �����������ߵĶ�����ͬ���������Ϊ���Ѻ������ߡ���������C1��y1=-2x2+4x+2��C2��y2=-x2+mx+nΪ���Ѻ������ߡ���
�����������ߵĶ�����ͬ���������Ϊ���Ѻ������ߡ���������C1��y1=-2x2+4x+2��C2��y2=-x2+mx+nΪ���Ѻ������ߡ������� ��1�������y1�������꣬Ȼ���������������ߵĶ���������ͬ�����m��n��ֵ��
��2����A��a��-a2+2a+3������OQ=x��AQ=-a2+2a+3��Ȼ��õ�OQ+AQ��a�ĺ�����ϵʽ����������䷽�������OQ+AQ����ֵ��
��3������BC������B����B��D��CM������ΪD��������֤����BCM�ա�MDB�䣬��ȫ�������ε����ʵõ�BC=MD��CM=B��D�����M������Ϊ��1��a�������ú�a��ʽ�ӿɱ�ʾ����B������꣬����B���������������ߵĽ���ʽ�����a��ֵ���Ӷ��õ���M�����꣮
��� �⣺��1����y1=-2x2+4x+2=-2��x-1��2+4��
��������C1�Ķ�������Ϊ��1��4����
��������C1��C2������ͬ��
��$\frac{-m}{-1��2}$=1��-1+m+n=4��
��ã�m=2��n=3��
��������C2�Ľ���ʽΪy2=-x2+2x+3��
��2����ͼ1��ʾ��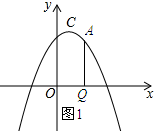
���A��������a��-a2+2a+3����
��AQ=-a2+2a+3��OQ=a��
��AQ+OQ=-a2+2a+3+a=-a2+3a+3=-��a-$\frac{3}{2}$��2+$\frac{21}{4}$��
�൱a=$\frac{3}{2}$ʱ��AQ+OQ�����ֵ�����ֵΪ$\frac{21}{4}$��
��3����ͼ2��ʾ������BC������B����B��D��CM������ΪD��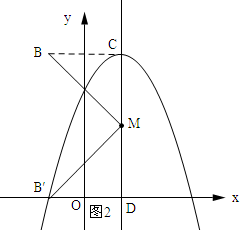
��B��-1��4����C��1��4���������ߵĶԳ���Ϊx=1��
��BC��CM��BC=2��
�ߡ�BMB��=90�㣬
���BMC+��B��MD=90�㣮
��B��D��MC��
���MB��D+��B��MD=90�㣮
���MB��D=��BMC��
�ڡ�BCM�͡�MDB���У�$\left\{\begin{array}{l}{��MB��D=��BMC}\\{��BCM=��MDB��}\\{BM=MB��}\end{array}\right.$��
���BCM�ա�MDB�䣮
��BC=MD��CM=B��D��
���M��������1��a������B��D=CM=4-a��MD=CB=2��
���B���������a-3��a-2����
��-��a-3��2+2��a-3��+3=a-2��
�����ã�a2-7a+10=0��
���a=2����a=5��
��a=2ʱ��M������Ϊ��1��2����
��a=5ʱ��M������Ϊ��1��5����
������������M������Ϊ��1��2����1��5��ʱ��B��ǡ������������C2�ϣ�
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˶��κ����Ķ������깫ʽ�����κ�����ͼ������ʡ�ȫ�������ε����ʺ��ж�������ͼ���ϵ�������뺯������ʽ�Ĺ�ϵ���ú�a��ʽ�ӱ�ʾ��B��������ǽ���Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ƽ���ı��εĶԽ������ | B�� | ���εĶԽ����ഹֱ | ||
| C�� | ���εĶԽ����ഹֱ��ƽ�� | D�� | �Խ�����ȵ��ı����Ǿ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
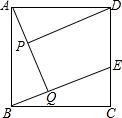 ��֪����ͼ����������ABCD�У���E�ڱ�CD�ϣ�AQ��BE�ڵ�Q��DP��AQ�ڵ�P��
��֪����ͼ����������ABCD�У���E�ڱ�CD�ϣ�AQ��BE�ڵ�Q��DP��AQ�ڵ�P���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
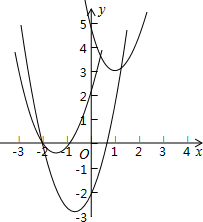 ��ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬������y=ax2+bx+5������M��1��3����N��3��5��
��ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬������y=ax2+bx+5������M��1��3����N��3��5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪������y=x2+bx��ֱ��y=2x+4����A��a��8����B���㣬��P����������A��B֮���һ�����㣬����P�ֱ���x�ᡢy���ƽ������ֱ��AB���ڵ�C�͵�E��
��ͼ����֪������y=x2+bx��ֱ��y=2x+4����A��a��8����B���㣬��P����������A��B֮���һ�����㣬����P�ֱ���x�ᡢy���ƽ������ֱ��AB���ڵ�C�͵�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 39 | B�� | 36 | C�� | 35 | D�� | 34 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com