
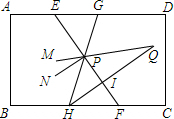
 如图,AD∥BC,EF、HG交于点P,HI平分∠GHF,PM平分∠EPH,HI交PM的反向延长线于Q,PN∥HI,则:①若∠EGP=∠GEP,则PM∥AD;②∠GEP=2∠MPN;③∠EPN=2∠Q,其中正确的是②.
如图,AD∥BC,EF、HG交于点P,HI平分∠GHF,PM平分∠EPH,HI交PM的反向延长线于Q,PN∥HI,则:①若∠EGP=∠GEP,则PM∥AD;②∠GEP=2∠MPN;③∠EPN=2∠Q,其中正确的是②. 分析 根据角平分线的定义得到∠EPM=∠MPH,若∠EGP=∠GEP,不能得到证明平行线的条件,①错误;根据角平分线的定义得到∠MPH=$\frac{1}{2}$∠EPH,∠PHQ=$\frac{1}{2}∠$PHF,根据外角的性质得到∠MPH=∠PHQ+∠Q,∠EPH=∠PHF+∠PFH,等量代换得到∠PFH=2∠Q,根据平行线的性质得到∠GEP=∠PFH,∠MPN=∠Q,等量代换得到∠GEP=2∠MPN,②正确;由于∠EPN=∠EPM+∠MPN=∠EPM+∠Q,而∠EPM=∠MPH≠∠MPN≠∠Q,于是得到∠EPN≠2∠Q,③错误.
解答 解:∵PM平分∠EPH,
∴∠EPM=∠MPH,
若∠EGP=∠GEP,
不能证得∠EGP=∠MPH,或∠GEP=∠EPM,
∴①错误;
∵PM平分∠EPH,
∴∠MPH=$\frac{1}{2}$∠EPH,
∵HI平分∠GHF,
∴∠PHQ=$\frac{1}{2}∠$PHF,
∵∠MPH=∠PHQ+∠Q,∠EPH=∠PHF+∠PFH,
∴$\frac{1}{2}$∠EPH=$\frac{1}{2}∠$PHF+∠Q=$\frac{1}{2}$(∠PHF+∠PFH),
∴∠PFH=2∠Q,
∵AD∥BC,
∴∠GEP=∠PFH,
∵PN∥HQ,
∴∠MPN=∠Q,
∴∠GEP=2∠MPN,②正确;
∵∠EPN=∠EPM+∠MPN=∠EPM+∠Q,
∵∠EPM=∠MPH≠∠MPN≠∠Q,
∴∠EPN≠2∠Q,③错误;
故答案为:②.
点评 本题考查了平行线的判定和性质,角平分线的定义,三角形的外角的性质,根据平行线的性质证得∠MPN=∠Q是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
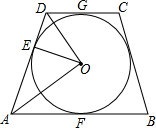 在四边形ABCD中,AB∥CD,⊙O分别与AD、AB、CD相切于E、F、G,连接OA、OD、OE.求证:∠AOE=$\frac{1}{2}$∠ADC.
在四边形ABCD中,AB∥CD,⊙O分别与AD、AB、CD相切于E、F、G,连接OA、OD、OE.求证:∠AOE=$\frac{1}{2}$∠ADC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在旷野上,一个人骑马从A出发,他先使马从A出发,他先使马到草地边l1吃草,再到河边l2饮水,最后返回A,他是怎样走才能使总路程最短?
如图,在旷野上,一个人骑马从A出发,他先使马从A出发,他先使马到草地边l1吃草,再到河边l2饮水,最后返回A,他是怎样走才能使总路程最短?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
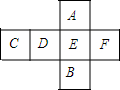 如图,是一个棱柱的平面展开图,每个面上都标上了字母,请根据要求回答下列问题.
如图,是一个棱柱的平面展开图,每个面上都标上了字母,请根据要求回答下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com