
【题目】为更新果树品种,某果园计划新购进A,B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种树苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.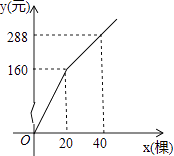
(1)求y与x的函数关系式;
(2)若在购买计划中,B种树苗的数量不超过35棵,但不少于A种树苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
【答案】
(1)解:设y与x的函数关系式为:y=kx+b,
当0≤x≤20时,把(0,0),(20,160)代入y=kx+b中,
得: ![]() ,解得:
,解得: ![]() ,
,
此时y与x的函数关系式为y=8x;
当20≤x时,把(20,160),(40,288)代入y=kx+b中,
得: ![]() ,解得:
,解得: ![]() ,
,
此时y与x的函数关系式为y=6.4x+32.
综上可知:y与x的函数关系式为y= ![]()
(2)解:∵B种苗的数量不超过35棵,但不少于A种苗的数量,
∴ ![]() ,
,
∴22.5≤x≤35,
设总费用为W元,则W=6.4x+32+7(45﹣x)=﹣0.6x+347,
∵k=﹣0.6,
∴y随x的增大而减小,
∴当x=35时,W总费用最低,W最低=﹣0.6×35+347=326(元)
【解析】(1)分为x≤20和20<x≤40两种情况,然后设y与x的函数关系式为:y=kx+b,然后找出两种情况下函数图像经过的点的坐标,最后,利用待定系数法求解即可;
(2)首先依据B种苗的数量不超过35棵,但不少于A种苗的数量可得出关于x的一元一次不等式组,从而可求得x的取值范围,再根据“所需费用为W=A种树苗的费用+B种树苗的费用”可得出W关于x的函数关系式,最后,再根据一次函数的性质以及自变量x的取值范围求解即可.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图.
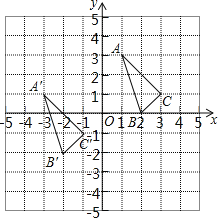
(1)分别写出下列各点的坐标: A′ ;B′ ;C′ ;
(2)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校要建一个面积是81平方米的草坪,草坪周围用铁栅栏围绕,现有两种方案:有人建议建成正方形,也有人建议建成圆形,如果从节省铁栅栏费用的角度考虑(栅栏周长越小,费用越少),你选择哪种方案?请说明理由.(π取3)
查看答案和解析>>
科目:初中数学 来源: 题型:
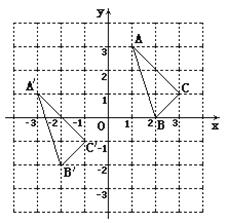
【题目】△ A B C与![]() 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.
(1)分别写出下列各点的坐标: ![]() ______ ;
______ ; ![]() _______ ;
_______ ; ![]() _______ ;
_______ ;
(2)说明![]() 由△ A B C经过怎样的平移得到? ________________________________.
由△ A B C经过怎样的平移得到? ________________________________.
(3)若点![]() (
(![]() ,
, ![]() )是△ A B C内部一点,则平移后
)是△ A B C内部一点,则平移后![]() 内的对应点
内的对应点![]() 的坐标为 ________ ;
的坐标为 ________ ;
(4)求△ A B C的面积..
查看答案和解析>>
科目:初中数学 来源: 题型:
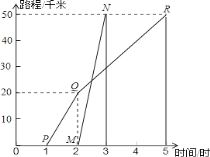
【题目】如图所示,甲、乙两人沿相同的路线由A到B行进,他们行进的路程与出发后的时间(h)之间的函数图象如图所示,根据图象信息,图中的折线PQR和线段MN分别表示甲乙所行驶的路程S和时间t的关系.
根据图象回答下列问题:
(1)A、B两地相距多远?
(2)甲和乙哪一个早到达B城?早多长时间?
(3)甲在QR段的速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N。

(1)求证:四边形CMAN是平行四边形。
(2)已知DE=4,FN=3,求BN的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线:y=ax2+bx+c(a>0)经过A(﹣1,1),B(2,4)两点,顶点坐标为(m,n),有下列结论: ①b<1;②c<2;③0<m< ![]() ;④n≤1.
;④n≤1.
则所有正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为![]() 、宽为
、宽为![]() 的长方形,沿图中虚线用剪刀剪成四块完全一样的小长方形,然后按图2的形状拼成一个正方形.
的长方形,沿图中虚线用剪刀剪成四块完全一样的小长方形,然后按图2的形状拼成一个正方形.
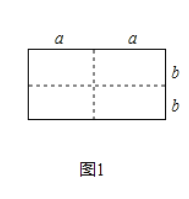
![]() 图2中的阴影部分的正方形的边长是 .
图2中的阴影部分的正方形的边长是 .
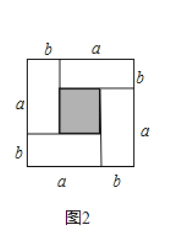
![]() 请用两种不同的方法表示图2中阴影部分的面积,并写出下列三个代数式:
请用两种不同的方法表示图2中阴影部分的面积,并写出下列三个代数式:![]() 之间的等量关系;
之间的等量关系;
![]() 利用
利用![]() 中的结论计算:
中的结论计算:![]() ,求
,求![]() 的值;
的值;
![]() 根据
根据![]() 中的结论,直接写出
中的结论,直接写出![]() 和
和![]() 之间的关系;若
之间的关系;若![]() ,分别求出
,分别求出![]() 和
和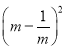 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】贵阳市某消防支队在一幢居民楼前进行消防演习,如图所示,消防官兵利用云梯成功救出在C处的求救者后,发现在C处正上方17米的B处又有一名求救者,消防官兵立刻升高云梯将其救出,已知点A与居民楼的水平距离是15米,且在A点测得第一次施救时云梯与水平线的夹角∠CAD=60°,求第二次施救时云梯与水平线的夹角∠BAD的度数(结果精确到1°).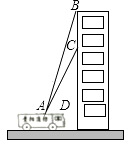
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com