
分析 (1)根据平方根的含义和求法,求出x的值是多少即可.
(2)首先计算乘方、开方和乘法,然后从左向右依次计算,求出算式的值是多少即可.
解答 解:(1)∵(x+1)2=64,
∴x+1=±8,
当x+1=8时,x=7;
当x+1=-8时,x=-8.
(2)(-2)3×$\sqrt{(-4)^{2}}$+$\root{3}{(-4)^{3}}$×($\frac{1}{2}$)2-$\sqrt{9}$.
=(-8)×4+(-4)×$\frac{1}{4}$-3
=-32-1-3
=-36
点评 此题主要考查了实数的运算,以及平方根的含义和求法,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.


科目:初中数学 来源: 题型:解答题
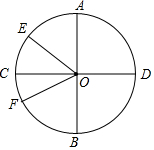 如图,圆O的直径为10cm,两条直径AB,CD相交成90°角,∠AOE=50°,OF是∠BOE的平分线.
如图,圆O的直径为10cm,两条直径AB,CD相交成90°角,∠AOE=50°,OF是∠BOE的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
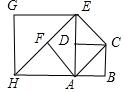 如图,在边长为1的正方形ABCD中,连结对角线AC,以AC为边作第二个正方形,连结对角线AE,以AE为边作第三个正方形…按此规律所作的第2017个正方形的边长是( )
如图,在边长为1的正方形ABCD中,连结对角线AC,以AC为边作第二个正方形,连结对角线AE,以AE为边作第三个正方形…按此规律所作的第2017个正方形的边长是( )| A. | 22016 | B. | 22016$\sqrt{2}$ | C. | 21008 | D. | 21008$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
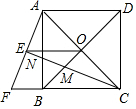 如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO,已知BD=2$\sqrt{2}$.
如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO,已知BD=2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
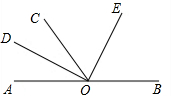 如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC.
如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知E、F、G、H分别是矩形四边AB、BC、CD、DA的中点,且四边形EFGH的周长为16cm,则矩形ABCD的对角线长等于8cm.
如图,已知E、F、G、H分别是矩形四边AB、BC、CD、DA的中点,且四边形EFGH的周长为16cm,则矩形ABCD的对角线长等于8cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com