如图，在梯形ABCD中，AD∥BC，对角线AC，BD相交于点E．若AE=4，CE=8，DE=3，梯形ABCD的高是
，面积是54．求证：AC⊥BD．
证明见解析.
解析试题分析：由AD∥BC，可证明△EAD∽△ECB，利用相似三角形的性质即可求出BE的长，过D作DF∥AC交BC延长线于F，则四边形ACFD是平行四边形，所以CF=AD，再根据勾股定理的逆定理证明BD⊥DF即可证明AC⊥BD.
试题解析：∵AD∥BC，∴△EAD∽△ECB. ∴AE：CE=DE：BE.
∵AE=4，CE=8，DE=3，∴BE=6.
∵S梯形=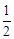
（AD+BC）×=54，∴AD+BC=15.
过D作DF∥AC交BC延长线于F，则四边形ACFD是平行四边形，
∴CF="AD." ∴BF=AD+BC=15.
在△BDF中，BD2+DF2=92+122=225，BF2=225，∴BD2+DF2=BF2. ∴BD⊥DF.
∵AC∥DF，∴AC⊥BD.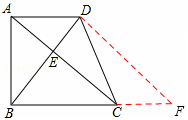
考点：1.梯形的性质；2.相似三角形的判定和性质；3.平行四边形的判定和性质；4.勾股定理的逆定理.
名校通行证有效作业系列答案科目：初中数学 来源： 题型：解答题
提出问题
如图1，在等边△ABC中，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等边△AMN，连结CN．求证：∠ABC=∠ACN．
类比探究
如图2，在等边△ABC中，点M是BC延长线上的任意一点（不含端点C），其它条件不变，（1）中结论∠ABC=∠ACN还成立吗？请说明理由．
拓展延伸
如图3，在等腰△ABC中，BA=BC，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等腰△AMN，使顶角∠AMN=∠ABC．连结CN．试探究∠ABC与∠ACN的数量关系，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
如图，在边长为4的正方形ABCD中，点P在AB上从A向B运动，连接DP交AC于点Q．
（1）试证明：无论点P运动到AB上何处时，都有△ADQ≌△ABQ；
（2）当点P在AB上运动到什么位置时，△ADQ的面积是正方形ABCD面积的
；
（3）若点P从点A运动到点B，再继续在BC上运动到点C，在整个运动过程中，当点P运动到什么位置时，△ADQ恰为等腰三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
在边长为6的菱形ABCD中，动点M从点A出发，沿A→B→C向终点C运动，连接DM交AC于点N．
（1）如图1，当点M在AB边上时，连接BN
①试说明：
；
②若∠ABC=60°，AM=4，求点M到AD的距离．
（2）如图2，若∠ABC=90°，记点M运动所经过的路程为x（6≤x≤12）．试问：x为何值时，△ADN为等腰三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：解答题
在△ABC中，∠ACB=90°，∠A＜45°，点O为AB中点，一个足够大的三角板的直角顶点与点O重合，一边OE经过点C，另一边OD与AC交于点M．
（1）如图1，当∠A=30°时，求证：MC2=AM2+BC2；
（2）如图2，当∠A≠30°时，（1）中的结论是否成立？如果成立，请说明理由；如果不成立，请写出你认为正确的结论，并说明理由；
（3）将三角形ODE绕点O旋转，若直线OD与直线AC相交于点M，直线OE与直线BC相交于点N，连接MN，则MN2=AM2+BN2成立吗？
答： （填“成立”或“不成立”）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
是等边三角形，点
、
分别在边
、
上，
．
∽△
；（2）如果
，
，求
的长．
