
 如图,PA、PB分别与⊙O相切于点A、B,PO的延长线交⊙O于点C,连接BC,OA.
如图,PA、PB分别与⊙O相切于点A、B,PO的延长线交⊙O于点C,连接BC,OA.分析 (1)根据切线长定理证明Rt△POA≌Rt△POB,再利用同弧所对的圆心角是圆周角的二倍可得结论;
(2)利用面积法求高线BE的长,利用勾股定理求OE,得CE的长,最后在Rt△OBE中,利用三角函数定义代入可得结果.
解答  证明:(1)连接OB,
证明:(1)连接OB,
∵PA、PB分别与⊙O相切于点A、B,
∴PA=PB,∠OBP=∠OAP=90°,
在Rt△POA和Rt△POB中,
∵$\left\{\begin{array}{l}{PA=PB}\\{PO=PO}\end{array}\right.$,
∴Rt△POA≌Rt△POB(HL),
∴∠POA=∠POB,
∵∠POB=2∠PCB,
∴∠POA=2∠PCB;
(2)过B作BE⊥PC于E,
∵PB=PA=4,OB=OA=3,
∴PO=5,
∴$\frac{1}{2}$PO•BE=$\frac{1}{2}$OB•PB,
∴BE=$\frac{12}{5}$,
由勾股定理得:OE=$\sqrt{{3}^{2}-(\frac{12}{5})^{2}}$=$\frac{9}{5}$,
∴CE=OC+OE=3+$\frac{9}{5}$=$\frac{24}{5}$,
在Rt△OBE中,tan∠PCB=$\frac{BE}{CE}$=$\frac{\frac{12}{5}}{\frac{24}{5}}$=$\frac{1}{2}$.
点评 本题考查了切线长定理、圆周角定理、三角形全等的性质和判定和勾股定理、三角函数,作辅助线构建直角三角形是第二问的关键,本题难度适中.


科目:初中数学 来源: 题型:解答题
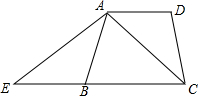 如图,在四边形ABCD中,AB=DC,延长线段CB到E,使BE=AD,连接AE,AC,∠ADC+∠ABC=180°.
如图,在四边形ABCD中,AB=DC,延长线段CB到E,使BE=AD,连接AE,AC,∠ADC+∠ABC=180°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在等腰直角三角形ABC中,∠ACB=90°,AB=8$\sqrt{2}$cm,点P(不与A,B重合)从点A出发,沿AB方向以$\sqrt{2}$cm/s的速度向终点B运动,在运动过程中,过点P作PQ⊥AB交射线BC于点Q,以线段PQ为边作等腰直角三角形PQR,且∠PQR=90°(点B,R位于PQ两侧),设△PQR与△ABC重叠部分图形的面积为S(cm2),点P的运动时间为t(s).
如图,在等腰直角三角形ABC中,∠ACB=90°,AB=8$\sqrt{2}$cm,点P(不与A,B重合)从点A出发,沿AB方向以$\sqrt{2}$cm/s的速度向终点B运动,在运动过程中,过点P作PQ⊥AB交射线BC于点Q,以线段PQ为边作等腰直角三角形PQR,且∠PQR=90°(点B,R位于PQ两侧),设△PQR与△ABC重叠部分图形的面积为S(cm2),点P的运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图.在平面直角坐标系内,△ABC三个顶点的坐标分别为A(1,-2),B(4,-1),C(3,-3)(正方形网格中,每个小正方形的边长都是1个单位长度).
如图.在平面直角坐标系内,△ABC三个顶点的坐标分别为A(1,-2),B(4,-1),C(3,-3)(正方形网格中,每个小正方形的边长都是1个单位长度).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知函数y=2+$\frac{4}{x}$.
已知函数y=2+$\frac{4}{x}$.| x | … | -8 | -4 | -3 | -2 | -1 | -$\frac{1}{2}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | 8 | … |
| y | … | $\frac{3}{2}$ | 1 | $\frac{2}{3}$ | 0 | -2 | -6 | 10 | 6 | 4 | $\frac{10}{3}$ | 3 | $\frac{5}{2}$ | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE,⑤CF=BD.正确的有( )个.
如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE,⑤CF=BD.正确的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知?ABCD的对角线AC与BD交于点O,下列结论不正确的是( )
已知?ABCD的对角线AC与BD交于点O,下列结论不正确的是( )| A. | 当AB=BC时,?ABCD是菱形 | B. | 当AC⊥BD时,?ABCD是菱形 | ||
| C. | 当OA=OB时,?ABCD是矩形 | D. | 当∠ABD=∠CBD时,?ABCD是矩形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com