

分析 【探究】由已知条件易证∠FDC=∠ACE,进而可证明△DFC≌△CEA,由全等三角形的性质:对应边相等即可得到DF=CE;
【应用】过点C作CG⊥AB,垂足为点G,由已知条件可以得到CA=CD,∠DFC=∠CGA,由CG⊥AB,DF⊥CE,交EC的延长线于点F,∠CEA=50°,∠ACD=50°,可以得到∠DCF=∠CAG,从而可以证得△CDF≌△ACG,由全等三角形的性质可以得到DF=CG,根据在△ABC中,AC=BC=5,AB=8,过点C作CG⊥AB,可以求得CG的长,从而得到DF的长.
解答 【探究】证明:
∵∠ACD=90°,
∴∠DCF+∠ACE=90°,
∵DF⊥CF,
∴∠DCF+∠FDC=90°,
∴∠FDC=∠ACE,
∵DF⊥CF,CE⊥AB,
∴∠AEC=∠DFC=90°,
在△DFC和△CEA中
$\left\{\begin{array}{l}{∠DFC=∠AEC=90°}\\{∠FDC=∠ACE}\\{DC=AC}\end{array}\right.$,
∴△DFC≌△CEA(AAS),
∴DF=CE;
【应用】过点C作CG⊥AB,垂足为点G,
∵CG⊥AB,DF⊥CE,交EC的延长线于点F,∠CEA=50°,∠ACD=50°,
∴∠CGA=∠CGE=∠DFC=90°,
∴∠GCE=∠CGE-∠CEA=90°-50°=40°,∠FDC+∠DCF=90°,
∵∠ECG+∠GCA+∠ACD+∠DCF=180°,
∴∠GCA+∠DCF=90°,
∴∠GCA=∠FDC,
在△CDF和△ACG中,
$\left\{\begin{array}{l}{∠GCA=∠FDC}\\{∠DFC=∠CGA}\\{CD=AC}\end{array}\right.$
∴△CDF≌△ACG(AAS),
∴DF=CG,
∵在△ABC中,AC=BC=5,AB=8,过点C作CG⊥AB,
∴AG=4,
∴CF=$\sqrt{A{C}^{2}-A{G}^{2}}$=3,
∴DF=3.
点评 本题考查全等三角形的判定和性质以及勾股定理的运用,解题的关键是正确做出题目的辅助线再找出题目中全等三角形需要的条件,题目的综合性较强,难度中等,是一道不错的中考试题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在玲玲家住宅楼CD的前面新建了一个大型商场AB,当光线与地面的夹角是22°时,商场在玲玲家楼上留下高2m的影子CE;而当光线与地面的夹角是45°时,商场楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).求商场AB的高度.(参考数据:sin22°≈$\frac{3}{8}$,cos22°≈$\frac{15}{16}$,tan22°≈$\frac{2}{5}$)
如图,在玲玲家住宅楼CD的前面新建了一个大型商场AB,当光线与地面的夹角是22°时,商场在玲玲家楼上留下高2m的影子CE;而当光线与地面的夹角是45°时,商场楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).求商场AB的高度.(参考数据:sin22°≈$\frac{3}{8}$,cos22°≈$\frac{15}{16}$,tan22°≈$\frac{2}{5}$)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,3) | B. | (-2,3) | C. | (2,-3) | D. | (2,-3)或(-2,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
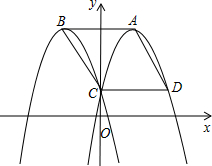 已知如图,抛物线C1:y=-x2+4x+1的顶点A在第一象限,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B,若点P是抛物线C1上的点,使得以A、B、C、P为顶点的四边形为平行四边形,则平行四边形ABCP的面积为8.
已知如图,抛物线C1:y=-x2+4x+1的顶点A在第一象限,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B,若点P是抛物线C1上的点,使得以A、B、C、P为顶点的四边形为平行四边形,则平行四边形ABCP的面积为8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
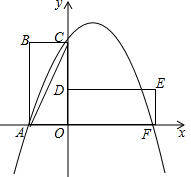 如图,在平面直角坐标系中,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=1,tan∠ACB=2,将矩形OABC绕点O按顺时针方向旋转90°后得到矩形ODEF.点A的对应点为点D,点B的对应点为点E,点C的对应点为点F,抛物线y=ax2+bx+2的图象过点A,C,F.
如图,在平面直角坐标系中,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=1,tan∠ACB=2,将矩形OABC绕点O按顺时针方向旋转90°后得到矩形ODEF.点A的对应点为点D,点B的对应点为点E,点C的对应点为点F,抛物线y=ax2+bx+2的图象过点A,C,F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com