练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    为落实校园“阳光体育”工程，某校计划购买篮球和排球共20个．已知篮球每个80元，排球每个60元．设购买篮球x个，购买篮球和排球的总费用y元．

    （1）求y与x之间的函数关系式；

    （2）如果要求篮球的个数不少于排球个数的3倍，应如何购买，才能使总费用最少？最少费用是多少元？


    解：（1）y＝80x＋60(20－x)＝1200＋20 x                     （2）x≥3(20－x)  解得x≥15                  

             要使总费用最少，x必须取最小值15            

             y＝1200＋20×15＝1500                        

    答：购买篮球15个，排球5个，才能使总费用最少 

    最少费用是1500元．                           

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，AB是⊙O的直径，AB=4，AC是弦，AC=，∠AOC=（    ）

        A. 120°       B. 130°       C. 140°        D. 150°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解二元一次方程组：

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    现定义运算“★”，对于任意实数a、b，都有a★b=，如：4★5=，若x★2=6，则实数x的值是（     ）

    A.或      B.4或     C.4或      D.或2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    化简：.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知点M（2，-3）与点N关于y轴对称，则N点的坐标为     (      )

       A．（2，3）           B.（-2，-3）            C.（3，2）      D.（3，-2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    双曲线的图像经过点（1，m），则m=_________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


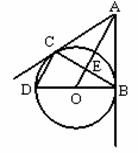
    如图10，从⊙O外一点A作⊙O的切线AB、AC，切点分别为B、C，且⊙O的直经BD=6，连结CD、AO、BC，且AO与BC相交于点E。

    （1）求证：CD∥AO；

    （2）设CD=x，AO=y，求y与x之间的函数关系式，并直接写出自变量x的取值范围；

    （3）请阅读下方资源链接内容。

    在（2）的基础上，若CD、AO的长

    分别为一元二次方程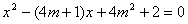的两个实数根，求AB的长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，直线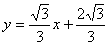与y轴相交于点D，点A1在直线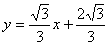上，点B1在X轴上，且△OA1B1是正三角形，记作第一个正三角形；然后过B1作B1A2//OA1

    与直线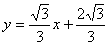相交于点A2，点B2在X轴上，再以B1A2为边作正三角形

    A2B2B1，记作第二个正三角形；同样过B2作B2A3//B1A2与直线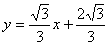相交

    于点A3，点B3在x轴上，再以B2A3为边作正三角形A3B3B2，记作第三个正三角形；…依此类推，则第n个正三角形的顶点An的纵坐标为            

     


    查看答案和解析>>

    同步练习册答案