练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
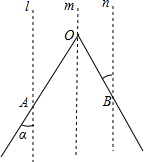
    4．如图，已知：∠AOB=60°，点A、B分别在∠AOB两边上，直线l、m、n分别过A、O、B三点，且满足直线l∥m∥n，OB与直线n所夹的角为25°，则∠α的度数为（　　）
    A．25°B．45°C．35°D．30°

    分析 先根据m∥n求出∠BCD的度数，再由△ABC是等边三角形求出∠ACB的度数，根据l∥m即可得出结论．

    解答 解：∵m∥n，边BO与直线n所夹的角为25°，
    ∴∠1=25°．
    ∵∠AOB=60°，
    ∴∠2=60°-25°=35°．
    ∵l∥m，
    ∴∠α=∠2=35°．
    故选C．

    点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，内错角相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

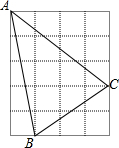    14．阅读：直角三角形具有下列性质，若直角三角形的两直角分别为a，b．斜边为c，则a2+b2=c2，利用这一性质．可求出某些线段的长，如图，正方形网格中，每个小正方形的边长均为1，则BC2=22+32，即BC=$\sqrt{2^2+3^2}$=$\sqrt{13}$，因3$＜\sqrt{13}＜$4，所以线段BC的长是无理数，请你利用以上阅读材料，判断图中线段AC、AB的长是有理数还是无理数，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．若am=-2，an=-$\frac{1}{2}$，则a2m+3n=-$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知a+b=3，ab=-2，求下列各式的值：
    （1）a2+b2            
    （2）（a-2）（b-2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算：
    （1）（x+y）（x2-xy+y2）
    （2）-12x2y•（$\frac{1}{3}$x3y2-$\frac{3}{4}{x}^{2}y$+$\frac{1}{6}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．计算：
    （1）-32+（π-2）0+（$\frac{1}{3}$）-2
    （2）5m•（-$\frac{2}{3}$abm2）•（-a2m）
    （3）（a-2b）（2a+b）-（a+2b）2
    （4）10$\frac{1}{9}$×9$\frac{8}{9}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，在?ABCD中，∠ABC=60°，BE平分∠ABC且交AD于点E，DF∥BE且交BC于点F．
    （1）求证：四边形BEDF是平行四边形；
    （2）求∠FDC的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．已知x+y=1，xy=-2，那么（2-x）（2-y）的值为（　　）
    A．-3B．-1C．0D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

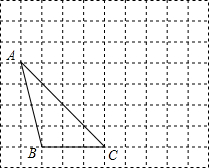    14．在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的位置如图所示，将△ABC先向右平移5个单位得△A1B1C1，再向上平移2个单位得△A2B2C2．
    （1）画出平移后的△A1B1C1及△A2B2C2；
    （2）平移过程中，线段AC扫过的面积是多少？

    查看答案和解析>>

    同步练习册答案