
 如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.
如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.分析 (1)如图1,证明△OMT≌△ONT,得∠MOT=∠NOT,再根据等腰△OMN三线合一的性质得MN⊥OT;
(2)①如图2,先根据勾股定理求AO的长,再利用勾股定理列方程求OC的长,则AC=OC+AO,代入得出结论;
②如图3,先证明△BEM∽△BDF,可得$\frac{BE}{BD}=\frac{EM}{DF}$,求出DF=9.6;再通过勾股定理求EF的长,则得BF的长,通过证明△BGF∽△EFD,得$\frac{BF}{DE}=\frac{FG}{DF}$,所以可以求FG的长,即点F到AB的距离.
解答  解:(1)如图1,连接MN、OT交于点A,
解:(1)如图1,连接MN、OT交于点A,
MN⊥OT,理由是:
∵OM=ON,TM=TN,OT=OT,
∴△OMT≌△ONT,
∴∠MOT=∠NOT,
∵OM=ON,
∴MN⊥OT;
(2)①如图2, ∵四边形ABCD为筝形,
∵四边形ABCD为筝形,
∴AC⊥BD,
∵AB=AD,
∴OB=OD=$\frac{1}{2}$BD=$\frac{1}{2}$×16=8,
由勾股定理得:AO=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
设OC=x,
∵∠ABC=90°,
∴BC2=AC2-AB2,BC2=OC2+OB2,
∴82+x2=(6+x)2-102,
解得:x=$\frac{32}{3}$,
∴AC=OA+OC=6+$\frac{32}{3}$=$\frac{50}{3}$;
②∵四边形ABED为菱形,
∴BE=AD=10,EM=AM=6,
∵∠FBD=∠FBD,∠BMC=∠BFD=90°,
∴△BEM∽△BDF,
∴$\frac{BE}{BD}=\frac{EM}{DF}$,
∴$\frac{10}{16}=\frac{6}{DF}$,
∴DF=9.6,
在Rt△DEF中,EF=$\sqrt{D{E}^{2}-D{F}^{2}}$=$\sqrt{1{0}^{2}-9.{6}^{2}}$=2.8,
∴BF=2.8+10=12.8,
∵∠BGF=∠EFD=90°,∠GBF=∠FED,
∴△BGF∽△EFD,
∴$\frac{BF}{DE}=\frac{FG}{DF}$,
∴FG=$\frac{BF•DF}{DE}$=$\frac{12.8×9.6}{10}$=12.288.
则点F到AB的距离为12.288.
点评 本题是四边形的综合题,考查了筝形的定义,并根据定义判断筝形的对角线互相垂直;本题还考查了全等三角形、相似三角形的性质和判定,多次运用相似三角形对应边的比和勾股定理求边长.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 已知正五边形ABCDE,请仅用无刻度直尺作图.
已知正五边形ABCDE,请仅用无刻度直尺作图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:∠ABC,按下列要求画出图形.
已知:∠ABC,按下列要求画出图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
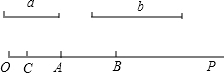 根据所示图形填空:
根据所示图形填空:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 身高(单位:米) | 1.60 | 1.62 | 1.65 | 1.70 | 1.76 | 1.80 | 1.85 | 1.90 |
| 人数 | 1 | 3 | 2 | 2 | 4 | 2 | 1 | 1 |
| A. | 1.73米,4个 | B. | 1.70米,1.76米 | C. | 1.73米,1.76米 | D. | 1.76米,4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,菱形ABCD中,AB=8,∠ABC=60°,E是CD的中点,在对角线AC有一动点P,在某个位置存在PD+PE的和最小,则这个最小值为4$\sqrt{7}$.
如图,菱形ABCD中,AB=8,∠ABC=60°,E是CD的中点,在对角线AC有一动点P,在某个位置存在PD+PE的和最小,则这个最小值为4$\sqrt{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 选手 | 甲 | 乙 | 丙 | 丁 |
| 方差(环2) | 0.035 | 0.016 | 0.022 | 0.025 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com