
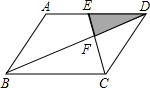
 如图,?ABCD中,E为AD的中点.已知△DEF的面积为S,则四边形ABFE的面积为( )
如图,?ABCD中,E为AD的中点.已知△DEF的面积为S,则四边形ABFE的面积为( )| A、5S | B、6S | C、7S | D、8S |
| DE |
| BC |
| 1 |
| 2 |
| 1 |
| 2 |



科目:初中数学 来源: 题型:
| A、y=2x-3 |
| B、y=3x-2 |
| C、y=2x+3 |
| D、y=3x+2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
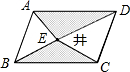 如图,有位农场主有一大片田地,其形状恰好是一个平行四边形,并且在对角线BD上有一口水井E.农场主临死前留下遗嘱,把两块三角形的田地(即图7中阴影部分)给小儿子,剩下的全部给大儿子,至于水井E,正好两儿子共用,由于平行四边形两边长不同,所以遗嘱公布之后,亲友们七嘴八舌,议论纷纷,认为这个分配不公平,那么你认为
如图,有位农场主有一大片田地,其形状恰好是一个平行四边形,并且在对角线BD上有一口水井E.农场主临死前留下遗嘱,把两块三角形的田地(即图7中阴影部分)给小儿子,剩下的全部给大儿子,至于水井E,正好两儿子共用,由于平行四边形两边长不同,所以遗嘱公布之后,亲友们七嘴八舌,议论纷纷,认为这个分配不公平,那么你认为查看答案和解析>>
科目:初中数学 来源: 题型:
| A、53天 | B、54天 |
| C、55天 | D、56天 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com