
| A. | a:b:c=3:5:6 | B. | a2-c2=b2 | C. | ∠A-∠B=∠C | D. | a=$\sqrt{7}$,b=3,c=4 |
分析 利用直角三角形的定义和勾股定理的逆定理逐项判断即可.
解答 解:A、不妨设a=3,b=5,c=6,此时a2+b2=34,而c2=36,即a2+b2≠c2,故△ABC不是直角三角形;
B、由条件可得到a2=c2+b2,满足勾股定理的逆定理,故△ABC是直角三角形;
C、由条件可得∠A=∠B+∠C,且∠A+∠B+∠C=180°,可求得∠A=90°,故△ABC为直角三角形;
D、由条件有a2+b2=($\sqrt{7}$)2+32=16=42=c2,满足勾股定理的逆定理,故△ABC是直角三角形.
故选A.
点评 本题主要考查直角三角形的判定方法,掌握判定直角三角形的方法是解题的关键,可以利用定义也可以利用勾股定理的逆定理.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
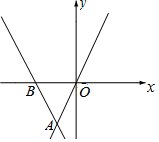 如图,直线y=kx+b经过点A(-1,m)和点B(-2,0),直线y=2x过点A,则不等式2x<kx+b<0的解集为( )
如图,直线y=kx+b经过点A(-1,m)和点B(-2,0),直线y=2x过点A,则不等式2x<kx+b<0的解集为( )| A. | x<-2 | B. | -2<x<-1 | C. | -2<x<0 | D. | -1<x<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由5x=4x+1可得4x-5x=1 | B. | 由3(x-1)-2(2x-3)=1可得3x-3-4x-6=1 | ||
| C. | 由$\frac{x+2}{4}$-1=$\frac{2x-3}{6}$可得3(x+2)-1=2(2x-3) | D. | 由$\frac{1}{2}$x=$\frac{1}{4}$可得x=$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
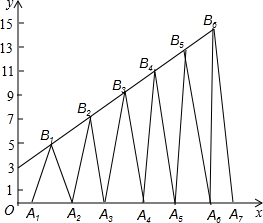 如图,已知B1(1,y1),B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2017-S2016=4037-8072a.
如图,已知B1(1,y1),B2(2,y2)B3(3,y3)…在直线y=2x+3上,在x轴上取点A1,使OA1=a(0<a<1);作等腰△A1B1A2面积为S1,等腰△A2B2A3面积为S2…;求S2017-S2016=4037-8072a.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1,1,2 | B. | 1,2,3 | C. | 1,$\sqrt{2}$,$\sqrt{3}$ | D. | 2,3,4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com