
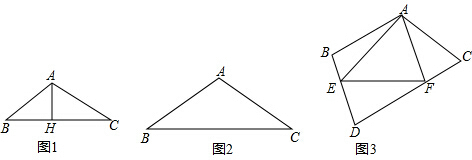
分析 (1)根据等腰三角形的性质得到BH=$\frac{1}{2}$BC=7cm,由勾股定理得到AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=$\sqrt{{8}^{2}-{7}^{2}}$=$\sqrt{15}$,根据三角形的面积公式即可得到结论;
(2)根据等边对等角可得∠B=∠C,然后表示出BD、BP、PC、CQ,再根据全等三角形对应边相等,分①BD、PC是对应边,②BD与CQ是对应边两种情况讨论求解即可;
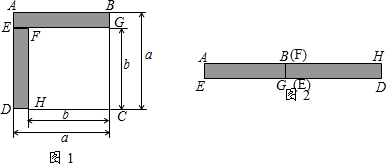
(3)延长DC到G使CG=BE,根据全等三角形的性质得到∠CAG=∠BAE,AE=AG,根据已知条件得到∠GAF=∠EAF,根据全等三角形的性质得到EF=FG,于是得到结论.
解答 解:(1)∵AB=AC=8cm,AH⊥BC于H,
∴BH=$\frac{1}{2}$BC=7cm,
∴AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=$\sqrt{{8}^{2}-{7}^{2}}$=$\sqrt{15}$,
设AB边上的高为h,
∴S△ABC=$\frac{1}{2}$AB•h=$\frac{1}{2}$BC•AH,
∴h=$\frac{7\sqrt{15}}{4}$,
∴AB边上的高的长为$\frac{7\sqrt{15}}{4}$;
(2)解:∵AB=8cm,BC=14cm,点D为AB的中点,
∴BD=$\frac{1}{2}$×8=4cm,
设点P、Q的运动时间为t,则BP=3t,
PC=(14-3t)cm,
①当BD=PC时,14-3t=4,
解得:t=$\frac{10}{3}$,
则BP=CQ=3t=10,(不合题意,舍去),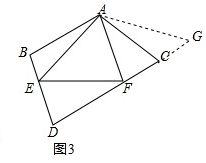
②当BP=PC时,∵BC=14cm,
∴BP=PC=7cm,
∴t=7÷3=$\frac{7}{3}$(秒),
故点Q的运动速度为4÷$\frac{7}{3}$=$\frac{12}{7}$(厘米/秒);
∴当点Q的运动速度为$\frac{12}{7}$(厘米/秒)时,△BPD与△CQP全等;
(3)延长DC到G使CG=BE,
∵∠ABD+∠ACD=180°,∠ACD+∠ACG=180°,
∴∠B=∠ACG,
在△ABE与△ACG中,$\left\{\begin{array}{l}{AB=AC}\\{∠B=∠ACG}\\{BE=CG}\end{array}\right.$,
∴△ABE≌△ACG,
∴∠CAG=∠BAE,AE=AG,
∵∠EAF=$\frac{1}{2}∠BAC$,
∴∠GAF=∠EAF,
在△AEF与△AFG中,$\left\{\begin{array}{l}{AE=AG}\\{∠EAF=∠FAG}\\{AF=AF}\end{array}\right.$,
∴△AEF≌△AFG,
∴EF=FG,
∵FG=CF+CG=CF+BE,
∴BE+FC=EF.
点评 本题考查了全等三角形的判定和性质,等腰三角形的性质,勾股定理,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,锐角∠C=θ°,BC=a,AC=b.
如图,在△ABC中,锐角∠C=θ°,BC=a,AC=b.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知点A(1,2),B(2,1),若点P是x轴上动点,点Q是y轴上动点,点P满足|PA-PB|的值最大,点Q满足QA+QB的值最小,则PQ=$\frac{\sqrt{106}}{3}$.
如图,已知点A(1,2),B(2,1),若点P是x轴上动点,点Q是y轴上动点,点P满足|PA-PB|的值最大,点Q满足QA+QB的值最小,则PQ=$\frac{\sqrt{106}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com