
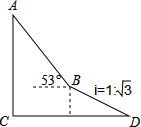 如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈$\frac{4}{3}$,计算结果用根号表示,不取近似值).
如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈$\frac{4}{3}$,计算结果用根号表示,不取近似值). 分析 如图作BN⊥CD于N,BM⊥AC于M,先在RT△BDN中求出线段BN,在RT△ABM中求出AM,再证明四边形CMBN是矩形,得CM=BN即可解决问题.
解答 解:如图作BN⊥CD于N,BM⊥AC于M. 在RT△BDN中,BD=30,BN:ND=1:$\sqrt{3}$,
在RT△BDN中,BD=30,BN:ND=1:$\sqrt{3}$,
∴BN=15,DN=15$\sqrt{3}$,
∵∠C=∠CMB=∠CNB=90°,
∴四边形CMBN是矩形,
∴CM=BN=15,BM=CN=60$\sqrt{3}$-15$\sqrt{3}$=45$\sqrt{3}$,
在RT△ABM中,tan∠ABM=$\frac{AM}{BM}$=$\frac{4}{3}$,
∴AM=60$\sqrt{3}$,
∴AC=AM+CM=15+60$\sqrt{3}$.
点评 本题考查解直角三角形、仰角、坡度等概念,解题的关键是添加辅助线构造直角三角形,记住坡度的定义,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
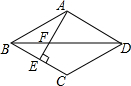 如图,BD是菱形ABCD的对角线,AE⊥BC于点E,交BD于点F,且E为BC的中点,则cos∠BFE的值是( )
如图,BD是菱形ABCD的对角线,AE⊥BC于点E,交BD于点F,且E为BC的中点,则cos∠BFE的值是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )
如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( )| A. | 12.5° | B. | 15° | C. | 20° | D. | 22.5° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
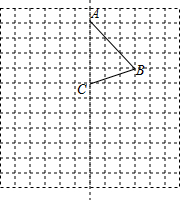 如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.
如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
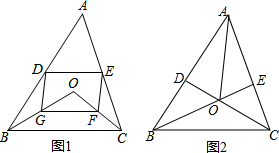 点D,E分别是△ABC的边AB,AC的中点.
点D,E分别是△ABC的边AB,AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 41×107 | B. | 4.1×108 | C. | 4.1×109 | D. | 0.41×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
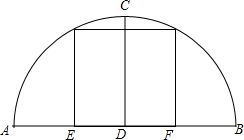 如图为一圆弧形拱桥,桥下水面宽为AB=24米,拱顶高出水面CD=8米.现有一艘宽EF=8米,且船舱顶部为矩形的货船要经过这里,那么货船高出水面的部分最多不能超过多少米?
如图为一圆弧形拱桥,桥下水面宽为AB=24米,拱顶高出水面CD=8米.现有一艘宽EF=8米,且船舱顶部为矩形的货船要经过这里,那么货船高出水面的部分最多不能超过多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com