
【题目】如图,把△ABC 绕点 A 顺时针旋转 n 度(0<n<180)后得到△ADE,并使点 D 落在 AC 的延长线上.
(1)若∠B=17°,∠E=55°,求 n;
(2)若 F 为 BC 的中点,G 为 DE 的中点,连 AG、AF、FG,求证:△AFG 为等腰三角形.

【答案】(1)108°(2)证明见解析
【解析】
(1)根据旋转的性质得到∠ACB=∠E=55°,根据三角形的内角和得到∠
BAC=180°﹣55°﹣17°=108°,于是得到结论;
(2)根据旋转的性质得到 AB=AD BC=DE,∠B=∠D,根据线段中点的定义得到 BF=![]() BC DG=
BC DG=![]() DE,根据全等三角形的性质即可得到结论.
DE,根据全等三角形的性质即可得到结论.
(1)∵△ADE 是由△ABC 旋转而来,
∴∠ACB=∠E=55°,
又∵∠B=17°,
∴∠BAC=180°﹣55°﹣17°= 108°,
∵D 落在 AC 延长线上,
∴∠BAC 即为旋转角,
∴n=108°;
(2)证明:∵△ADE 是由△ABC 旋转而来,
∴AB=AD BC=DE,∠B=∠D,
∵F、G 分别是 BC、DE 的中点,
∴BF= ![]() BC DG=
BC DG= ![]() DE,
DE,
∴BF=DG,
在△ABF 与△ADG 中
∴△ABF≌△ADG(SAS),
∴AF=AG,
∴△ADF 是等腰三角形.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,利用一面院墙,用篱笆围成一个外形为矩形的花圃,花圃的面积为S平方米,平行于院墙的一边长为x米.
(1)若院墙可利用最大长度为10米,篱笆长为24米,花圃中间用一道篱笆间隔成两个小矩形,求S与x之间的函数关系;
(2)在(1)的条件下,若围成的花圃面积为45平方米,求AB的长;
(3)在(1)的条件下,能否围成面积比45平方米更大的花圃?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=-x2+2x+3.
(1)求函数图像的顶点坐标,并画出这个函数的图像;
(2)根据图像,直接写出:
①当函数值y为正数时,自变量x的取值范围;
②当-2<x<2时,函数值y的取值范围;
③若经过点(0,k)且与x轴平行的直线l与y=-x2+2x+3的图像有公共点,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为正方形ABCD的中心,AD=1,BE平分∠DBC交DC于点E,延长BC到点F,使BD=BF,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:OH∥BF;②OG:GH=2:1;③GH=![]() ;④∠CHF=2∠EBC;⑤CH2=HEHB.正确结论的个数为( )
;④∠CHF=2∠EBC;⑤CH2=HEHB.正确结论的个数为( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读资料)
同学们,我们学过用配方法解一元二次方程,也可用配方法求代数式的最值.
(1)求4x2+16x+19的最小值.
解:4x2+16x+19=4x2+16x+16+3=4(x+2)2+3
因(x+2)2大于等于0,所以4x2+16x+19大于等于3,即4x2+16x+19的最小值是3.此时,x=﹣2
(2)求﹣m2﹣m+2的最大值
解:﹣m2﹣m+2=﹣(m2+m)+2=﹣![]()
因![]() 大于等于0,所以﹣
大于等于0,所以﹣![]() 小于等于0,所以﹣
小于等于0,所以﹣![]()
![]()
小于等于![]() ,即﹣m2﹣m+2的最大值是
,即﹣m2﹣m+2的最大值是![]() ,此时,m=﹣
,此时,m=﹣![]() .
.
(探索发现)

如图①,是一张直角三角形纸片,∠B=90°,AB=8,BC=6,小明想从中剪出一个以∠B为内角且面积最大的矩形,经过多次操作发现,当沿着中位线DE、EF剪下时,所得的矩形的面积最大.下面给出了未写完的证明,请你阅读下面的证明并写出余下的证明部分,并求出矩形的最大面积与原三角形面积的比值.
解:在AC上任取点E,作ED⊥BC,EF⊥AB,得到矩形BDEF.设EF=x
易证△AEF∽△ACB,则![]() ,
,![]() ,
,![]() ,
,![]() …
…
请你写出剩余部分
(拓展应用)
如图②,在△ABC中,BC=a,BC边上的高AD=h,矩形PQMN的顶点P、N分别在边AB、AC上,顶点Q、M在边BC上,则矩形PQMN面积的最大值为 .(用含a,h的代数式表示)
(灵活应用)
如图③,有一块“缺角矩形”ABCDE,AB=32,BC=40,AE=20,CD=16,小明从中剪出了一个面积最大的矩形(∠B为所剪出矩形的内角),该矩形的面积为 .(直接写出答案)
(实际应用)
如图④,现有一块四边形的木板余料ABCD,经测量AB=70cm,BC=108cm,CD=76cm,且∠B=∠C=60°,木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN,该矩形的面积为 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,E是正方形ABCD边AB上的一点,连接BD、DE,将∠BDE绕点D逆时针旋转90°,旋转后角的两边分别与射线BC交于点F和点G.
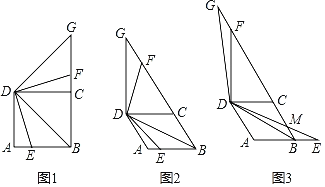
①线段DB和DG的数量关系是 ;
②写出线段BE,BF和DB之间的数量关系.
(2)当四边形ABCD为菱形,∠ADC=60°,点E是菱形ABCD边AB所在直线上的一点,连接BD、DE,将∠BDE绕点D逆时针旋转120°,旋转后角的两边分别与射线BC交于点F和点G.
①如图2,点E在线段AB上时,请探究线段BE、BF和BD之间的数量关系,写出结论并给出证明;
②如图3,点E在线段AB的延长线上时,DE交射线BC于点M,若BE=1,AB=2,直接写出线段GM的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x﹣![]() x2刻画,斜坡可以用一次函数y=
x2刻画,斜坡可以用一次函数y=![]() x刻画,下列结论错误的是( )
x刻画,下列结论错误的是( )

A. 当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m
B. 小球距O点水平距离超过4米呈下降趋势
C. 小球落地点距O点水平距离为7米
D. 斜坡的坡度为1:2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com