
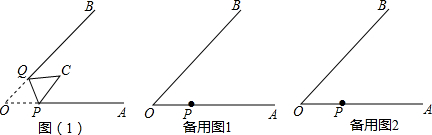
分析 (1)①由平行线的性质得出∠O=∠CPA,由折叠的性质得出∠C=∠O,OP=CP,证出∠CPA=∠C,得出OP∥QC,证出四边形OPCQ是菱形,得出OQ=OP=2cm即可;
②当PC⊥QB时,分两种情况:设OQ=xcm,证出△OPM是等腰直角三角形,得出OM=$\frac{\sqrt{2}}{2}$OP=$\sqrt{2}$,QM=$\sqrt{2}$-x,证出△CQM是等腰直角三角形,得出QC=$\sqrt{2}$QM,得出方程x=$\sqrt{2}$($\sqrt{2}$-x),解方程即可;(ii)同(i)得出:OQ=2$\sqrt{2}$+2;即可得出结论;
(2)当折叠后重叠部分为等腰三角形时,符合条件的点Q共有5个;点C在∠AOB的内部或一边上时,由折叠的性质、三角形内角和定理以及解直角三角形即可求出OQ的长;点C在∠AOB的外部时,同理求出OQ的长即可.
解答 解:(1)①当PC∥QB时,∠O=∠CPA,
由折叠的性质得:∠C=∠O,OP=CP,
∴∠CPA=∠C,
∴OP∥QC,
∴四边形OPCQ是平行四边形,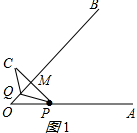
∴四边形OPCQ是菱形,
∴OQ=OP=2cm;
故答案为:2cm;
②当PC⊥QB时,分两种情况:
(i)如图1所示:设OQ=xcm,
∵∠O=45°,
∴△OPM是等腰直角三角形,
∴OM=$\frac{\sqrt{2}}{2}$OP=$\sqrt{2}$,
∴QM=$\sqrt{2}$-x,
由折叠的性质得:∠C=∠O=45°,CQ=OQ=x,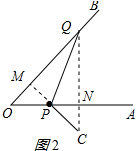
∴△CQM是等腰直角三角形,
∴QC=$\sqrt{2}$QM
∴x=$\sqrt{2}$($\sqrt{2}$-x),
解得:x=2$\sqrt{2}$-2,
即OQ=2$\sqrt{2}$-2;
(ii)如图2所示:同(i)得:OQ=2$\sqrt{2}$+2;
综上所述:当PC⊥QB时,OQ的长为2$\sqrt{2}$-2,或2$\sqrt{2}$+2.
(2)当折叠后重叠部分为等腰三角形时,符合条件的点Q共有5个;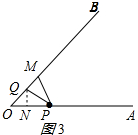
①点C在∠AOB的内部时,四边形OPCQ是菱形,OQ=OP=2cm;
②当点C在∠AOB的一边上时,△OPQ是等腰直角三角形,OQ=$\sqrt{2}$或2$\sqrt{2}$;
③当点C在∠AOB的外部时,分两种情况:
(i)如图3所示:PM=PQ,则∠PMQ=∠PQM=∠O+∠OPQ,
由折叠的性质得:∠OPQ=∠MPQ,
设∠OPQ=∠MPQ=x,
则∠PMQ=∠PQM=45°+x,
在△OPM中,由三角形内角和定理得:45°+x+x+45°+x=180°,
解得:x=30°,
∴∠OPQ=30°,
作QN⊥OP于N,设ON=a,
∵∠O=45°,
则QN=ON=a,OQ=$\sqrt{2}$a,PN=$\sqrt{3}$QN=$\sqrt{3}$a,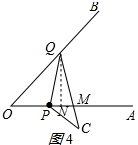
∵ON+PN=OP,
∴a+$\sqrt{3}$a=2,
解得:a=$\sqrt{3}$-1,
∴OQ=$\sqrt{2}$($\sqrt{3}$-1)=$\sqrt{6}$-$\sqrt{2}$;
(ii)如图4所示:PQ=MQ,作QN⊥OA于N,
同①得:OQ=$\sqrt{6}$+$\sqrt{2}$;
综上所述:当折叠后重叠部分为等腰三角形时,OQ的长为2cm或$\sqrt{2}$cm或2$\sqrt{2}$cm,或($\sqrt{6}$-$\sqrt{2}$)cm或($\sqrt{6}$+$\sqrt{2}$)cm.
点评 本题是三角形综合题目,考查了折叠的性质、等腰直角三角形的判定与性质、平行线的性质、等腰三角形的判定与性质、菱形的判定与性质、解直角三角形等知识;本题综合性强,有一定难度,熟练掌握折叠的性质,证明三角形是等腰直角三角形是解决问题的关键,注意分类讨论.


科目:初中数学 来源: 题型:解答题
| 读书册数 | 4 | 5 | 6 | 7 | 8 |
| 人数(人) | 6 | 4 | 10 | 12 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
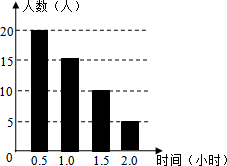 某校为了解学生课外阅读情况,随机调查了50名学生各自平均每天的课外阅读时间,并绘制成条形图,据此可以估计出该校所有学生平均每人每天的课外阅读时间为1小时.
某校为了解学生课外阅读情况,随机调查了50名学生各自平均每天的课外阅读时间,并绘制成条形图,据此可以估计出该校所有学生平均每人每天的课外阅读时间为1小时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
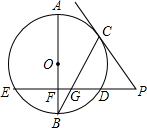 如图,已知AB是⊙O的直径,弦ED⊥AB于点F,点C是劣弧AD上的动点(不与点A、D重合),连接BC交ED于点G.过点C作⊙O的切线与ED的延长线交于点P.
如图,已知AB是⊙O的直径,弦ED⊥AB于点F,点C是劣弧AD上的动点(不与点A、D重合),连接BC交ED于点G.过点C作⊙O的切线与ED的延长线交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
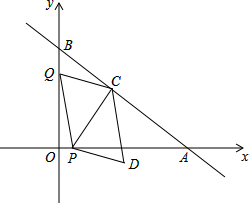 如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(8,0),B(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点Q从点B出发,沿射线BO方向以每秒2个单位的速度运动,过点P作PC⊥AB于点C,连接PQ,CQ,以PQ,CQ为邻边构造?PQCD,设点P运动的时间为t秒.
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(8,0),B(0,6),动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点Q从点B出发,沿射线BO方向以每秒2个单位的速度运动,过点P作PC⊥AB于点C,连接PQ,CQ,以PQ,CQ为邻边构造?PQCD,设点P运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{5}}$ | B. | $\sqrt{0.5}$ | C. | $\sqrt{5}$ | D. | $\sqrt{50}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com