
 ,第一批产品
,第一批产品 上市40天内全部售完.该公司对第一批产品
上市40天内全部售完.该公司对第一批产品 上市后的市场销售情况进行了跟踪调查,调查结果如图所示,其中图1中的折线表示的是市场日销售量与上市时间的关系;图2中的折线表示的是每件产品
上市后的市场销售情况进行了跟踪调查,调查结果如图所示,其中图1中的折线表示的是市场日销售量与上市时间的关系;图2中的折线表示的是每件产品 的销售利润与上市时间的关系.
的销售利润与上市时间的关系.
 的市场日销售量
的市场日销售量 与上市时间的关系式;
与上市时间的关系式; 上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?(说明理由)
上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?(说明理由)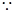 点(30,60)和(40,0)在图象上,
点(30,60)和(40,0)在图象上, 解得k1=-6,b=240.
解得k1=-6,b=240.

科目:初中数学 来源:不详 题型:解答题

 个平方单位?
个平方单位?查看答案和解析>>
科目:初中数学 来源:不详 题型:计算题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的解;
的解;查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A. m<0 | B. m>0 | C. m< | D. m> |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com