
 如图,已知等边△ABC的边长为2,E,F,G分别在边AB,BC,CA上,且△EFG也是等边三角形.
如图,已知等边△ABC的边长为2,E,F,G分别在边AB,BC,CA上,且△EFG也是等边三角形.分析 (1)根据等边三角形的性质得出∠A=∠B=∠FEG=60°,进而得出∠BFE=∠AEG,即可判断出,△BEF≌△AGE(AAS),结论得证;
(2)借助(1)的结论判断出S△BEF=S△CFG=S△AGE,再用x表示出△AEG的面积,最后用面积差建立方程求解即可.
解答 解:(1)∵△ABC、△EFG都是等边三角形,
∴EG=EF,∠A=∠B=∠FEG=60°,
在△BEF中,∠BEF+∠BFE=180°-∠B=120°,
∵∠BEF+∠AEG=180°-∠FEG=120°,
∴∠BFE=∠AEG,
在△BEF和△AGE中,$\left\{\begin{array}{l}{∠B=∠A=60°}\\{∠BFE=∠AEG}\\{EF=EG}\end{array}\right.$,
∴△BEF≌△AGE(AAS),
∴AG=BE,
(2)如图,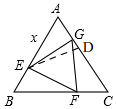 同(1)的方法得出,△BEF≌△CFG≌△AGE,
同(1)的方法得出,△BEF≌△CFG≌△AGE,
∴S△BEF=S△CFG=S△AGE,CG=AE=x,
∴AG=AC-x=2-x
过点E作ED⊥AC,在Rt△ADE中,∠A=60°,AE=x,
∴DE=$\frac{\sqrt{3}}{2}$x,
∵△ABC是等边三角形,
∴S△EFG=S△ABC-3S△AEG=$\frac{\sqrt{3}}{4}$×22-3×$\frac{1}{2}$×(2-x)×$\frac{\sqrt{3}}{2}$x=$\frac{3\sqrt{3}}{4}$(x-1)2+$\frac{\sqrt{3}}{4}$,
∵△EFG的面积为$\frac{\sqrt{3}}{4}$.
∴$\frac{3\sqrt{3}}{4}$(x-1)2+$\frac{\sqrt{3}}{4}$=$\frac{\sqrt{3}}{4}$,
∴x=1.
点评 此题是全等三角形的判定和性质,主要考查了等边三角形的性质,三角形的面积公式,解本题的关键是判断出∠BFE=∠AEG,也是解本题的难点,易错点是三角形EFG的面积式子的化简,用方程的思想解决问题是解这类问题常用的方法.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
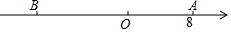 如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t<0)秒.
如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t<0)秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读下面的材料,回答问题:
阅读下面的材料,回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 作图题:有一张地图,图中有A,B,C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A地北偏东30°方向上,在B地的南偏东45°,请你用作图的方法确定C地的位置.(保留作图痕迹,不写作法)
作图题:有一张地图,图中有A,B,C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A地北偏东30°方向上,在B地的南偏东45°,请你用作图的方法确定C地的位置.(保留作图痕迹,不写作法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com