
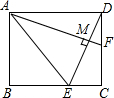
 如图所示,在矩形ABCD中,F是DC上的一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MD的长是( )
如图所示,在矩形ABCD中,F是DC上的一点,AE平分∠BAF交BC于点E,且DE⊥AF,垂足为点M,BE=3,AE=2$\sqrt{6}$,则MD的长是( )| A. | $\sqrt{15}$ | B. | $\frac{{\sqrt{15}}}{15}$ | C. | 1 | D. | $\frac{{\sqrt{15}}}{10}$ |
分析 设MD=a,MF=x,利用△ADM∽△DFM,列比例式得到a2=$\sqrt{15}$x,利用△DMF∽△DCE,列比例式得$\frac{MD}{DC}=\frac{FM}{EC}$,则$\frac{a}{\sqrt{15}}=\frac{x}{\sqrt{(a+3)^{2}-15}}$,得到a与x的关系式,列方程组化简可得x和a的值,得到答案.方法二:设DM=a,由△AEM≌△AEB,可得AB=AM=$\sqrt{15}$,BE=EM=3,由△ADM≌△DEC可得AD=DE=a+3,在Rt△ADM中,可得(a+3)2=a2+($\sqrt{15}$)2,由此即可解决问题.
解答 解:∵四边形ABCD是矩形,
∴∠B=90°,
∵AE平分∠BAF,且DE⊥AF,
∴AB=AM,BE=EM=3,
又∵AE=2$\sqrt{6}$,
∴AM=AB=$\sqrt{A{E}^{2}-B{E}^{2}}$=$\sqrt{(2\sqrt{6})^{2}-{3}^{2}}$=$\sqrt{15}$,
设MD=a,MF=x,
在△ADM和△DFM中,
∵∠AMD=∠DMF=90°,
∠ADM=∠DFM,
∴△ADM∽△DFM,
∴$\frac{DM}{AM}=\frac{FM}{DM}$,
∴DM2=AM•MF,
∴a2=$\sqrt{15}$x,
在Rt△DEC中,DE=3+a,DC=AB=$\sqrt{15}$,
由勾股定理得:EC=$\sqrt{(a+3)^{2}-(\sqrt{15})^{2}}$=$\sqrt{(a+3)^{2}-15}$,
在△DMF和△DCE中,
∵∠DMF=∠C=90°,
∠MDF=∠MDF,
∴△DMF∽△DCE,
∴$\frac{MD}{DC}=\frac{FM}{EC}$,
∴$\frac{a}{\sqrt{15}}=\frac{x}{\sqrt{(a+3)^{2}-15}}$,
∴$\left\{\begin{array}{l}{{a}^{2}=\sqrt{15}x}\\{\sqrt{15}x=a\sqrt{(a+3)^{2}-15}}\end{array}\right.$,
解之得:$\left\{\begin{array}{l}{a=1}\\{x=\frac{\sqrt{15}}{15}}\end{array}\right.$,
∴MD=1,
故答案选:C.
方法二:设DM=a,由△AEM≌△AEB,可得AB=AM=$\sqrt{15}$,BE=EM=3,
由△ADM≌△DEC可得AD=DE=a+3,
在Rt△ADM中,可得(a+3)2=a2+($\sqrt{15}$)2,解得a=1.
点评 本题考查了角平分线的性质以及三角形相似的判定方法,解题的关键在于利用三角形相似构造方程求得对应边的长度.


科目:初中数学 来源: 题型:解答题
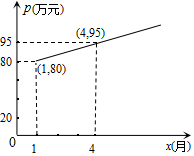 在气候对人类生存压力日趋加大的今天,发展低碳经济,全面实现低碳生活成为人们的共识,某企业采用技术革新,节能减排,经分析前5个月二氧化碳排放量y(吨)与月份x(月)之间的函数关系是y=-2x+50.
在气候对人类生存压力日趋加大的今天,发展低碳经济,全面实现低碳生活成为人们的共识,某企业采用技术革新,节能减排,经分析前5个月二氧化碳排放量y(吨)与月份x(月)之间的函数关系是y=-2x+50.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
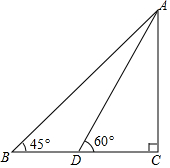 如图,某滑雪运动员训练时的斜坡示意图,某次训练拟将难度系数加大,决定将训练的斜坡的倾角由45°升为60°,已知原斜坡AB的长为3$\sqrt{6}$米,点B、D、C在同一水平地面上.若斜坡的正前方能有6米长的空地就能保证安全,已知原斜坡屈的前方有3米长的空地,进行这样的改造是否可行?并说明理由.(参考数据:$\sqrt{3}$=1.732,$\sqrt{6}$=2.449)
如图,某滑雪运动员训练时的斜坡示意图,某次训练拟将难度系数加大,决定将训练的斜坡的倾角由45°升为60°,已知原斜坡AB的长为3$\sqrt{6}$米,点B、D、C在同一水平地面上.若斜坡的正前方能有6米长的空地就能保证安全,已知原斜坡屈的前方有3米长的空地,进行这样的改造是否可行?并说明理由.(参考数据:$\sqrt{3}$=1.732,$\sqrt{6}$=2.449)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
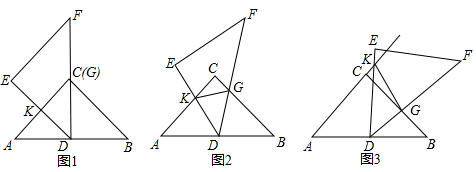
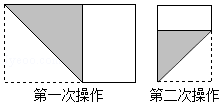 长为1,宽为a的矩形纸片($\frac{1}{2}$<a<1),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,求a的值.
长为1,宽为a的矩形纸片($\frac{1}{2}$<a<1),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,求a的值.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
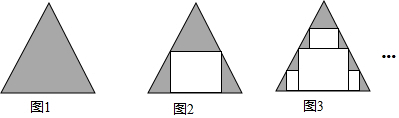
| A. | $\frac{\sqrt{3}}{{2}^{n-1}}{a}^{2}$ | B. | $\frac{\sqrt{3}}{{2}^{n}}{a}^{2}$ | C. | $\frac{\sqrt{3}}{{2}^{n+1}}{a}^{2}$ | D. | $\frac{\sqrt{3}}{{2}^{n+2}}{a}^{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6.6×103 | B. | 66×1010 | C. | 6.600×1011 | D. | 0.66×1012 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com