
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:解答题
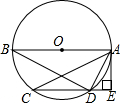 如图,在⊙O中,AB为直径,延长CD至E,使得AE⊥CE.
如图,在⊙O中,AB为直径,延长CD至E,使得AE⊥CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=4$\sqrt{3}$,∠BAD=60°,且AB>4$\sqrt{3}$.
如图,把△EFP按图示方式放置在菱形ABCD中,使得顶点E、F、P分别在线段AB、AD、AC上,已知EP=FP=4,EF=4$\sqrt{3}$,∠BAD=60°,且AB>4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在水平地面上竖立着一面墙AB,墙外有一盏路灯D.光线DC恰好通过墙的最高点B,且与地面形成37°角.墙在灯光下的影子为线段AC,并测得AC=5.5米.
如图,在水平地面上竖立着一面墙AB,墙外有一盏路灯D.光线DC恰好通过墙的最高点B,且与地面形成37°角.墙在灯光下的影子为线段AC,并测得AC=5.5米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
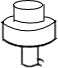 如图所示的容器内装满水,打开排水管,容器内的水匀速流出,则容器内液面的高度h随时间x变化的函数图象最接近实际情况的是( )
如图所示的容器内装满水,打开排水管,容器内的水匀速流出,则容器内液面的高度h随时间x变化的函数图象最接近实际情况的是( )| A. | 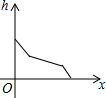 | B. | 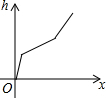 | C. | 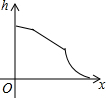 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
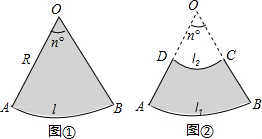
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com