
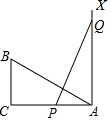
 如图,∠C=90°,AC=12,BC=6,AX⊥AC,点P和Q分别在线段AC和射线AX上运动,且PQ=AB,当点P从A点出发运动到C点或AC中点处时,△ABC≌△APQ.
如图,∠C=90°,AC=12,BC=6,AX⊥AC,点P和Q分别在线段AC和射线AX上运动,且PQ=AB,当点P从A点出发运动到C点或AC中点处时,△ABC≌△APQ. 分析 分两种情况:①当AP=BC=5时;②当AP=CA=10时;由HL证明Rt△ABC≌Rt△PQA(HL),即可得出结果.
解答 解:∵AX⊥AC,
∴∠PAQ=90°,
∴∠C=∠PAQ=90,
分两种情况:
①当AP=BC=6时,
在Rt△ABC和Rt△QPA中,$\left\{\begin{array}{l}{AB=PQ}\\{BC=AP}\end{array}\right.$,
∴Rt△ABC≌Rt△QPA(HL);
②当AP=CA=12时,
在△ABC和△PQA中,$\left\{\begin{array}{l}{AB=PQ}\\{AP=AC}\end{array}\right.$,
∴Rt△ABC≌Rt△PQA(HL);
综上所述:当点P运动到AP=6(此时P为AC的中点或12(此时P和C点重合)时,△ABC与△APQ全等;
故答案为:C点或AC中点.
点评 本题考查了直角三角形全等的判定方法;熟练掌握直角三角形全等的判定方法,本题需要分类讨论,难度适中.


科目:初中数学 来源: 题型:解答题
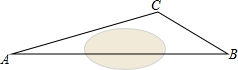 在一次课外实践活动中,数学兴趣小组要测量某公园人工湖两侧A、B两个凉亭之间的距离,如图,现测得∠ABC=30°,∠CAB=15°,AC=300米,请计算A、B两个凉亭之间的距离(结果精确到1米)
在一次课外实践活动中,数学兴趣小组要测量某公园人工湖两侧A、B两个凉亭之间的距离,如图,现测得∠ABC=30°,∠CAB=15°,AC=300米,请计算A、B两个凉亭之间的距离(结果精确到1米)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
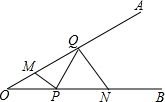 如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )
如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P,Q分别是边OB,OA上的动点,记∠OPM=α,∠OQN=β,当MP+PQ+QN最小时,则关于α,β的数量关系正确的是( )| A. | β-α=60° | B. | β+α=210° | C. | β-2α=30° | D. | β+2α=240° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.25 | B. | 4.25 | C. | 4.45 | D. | 4.75 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
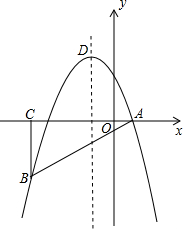 如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线y=-x2+bx+c经过A,B两点,其中点A,C的坐标分别为(1,0),(-4,0),抛物线的顶点为点D.
如图,在平面直角坐标系中,△ABC为等腰直角三角形,∠ACB=90°,抛物线y=-x2+bx+c经过A,B两点,其中点A,C的坐标分别为(1,0),(-4,0),抛物线的顶点为点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{19}{25}$ | B. | $\frac{3}{10}$ | C. | $\frac{47}{50}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com