
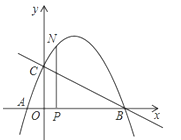
【题目】如图,抛物线与x轴交于点A(﹣![]() , 0),点B(2,0),与y轴交于点C(0,1),连接BC.
, 0),点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的解析式;
(2)N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣![]() <t<2),求△ABN的面积s与t的函数解析式;
<t<2),求△ABN的面积s与t的函数解析式;
(3)若0<t<2且t≠0时,△OPN∽△COB,求点N的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+1;(2)S=﹣
x+1;(2)S=﹣![]() t2+
t2+![]() t+
t+![]() ;(3)点N的坐标为(1,2)
;(3)点N的坐标为(1,2)
【解析】
(1)设抛物线的解析式为y=ax2+bx+c,然后利用待定系数法即可得;
(2)当﹣![]() <t<2时,点N在x轴上方,则NP等于点N的纵坐标,求出AB的长,然后利用三角形面积公式即可得;
<t<2时,点N在x轴上方,则NP等于点N的纵坐标,求出AB的长,然后利用三角形面积公式即可得;
(3)根据相似三角形的性质可得PN=2PO,由于PN=﹣![]() t2+
t2+![]() t+1,PO=|t|=t,可得关于t的方程,解这个方程即可解决这个问题.
t+1,PO=|t|=t,可得关于t的方程,解这个方程即可解决这个问题.
(1)设抛物线的解析式为y=ax2+bx+c,由题意可得: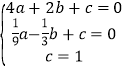 ,
,
解得: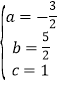 ,
,
∴抛物线的函数关系式为y=﹣![]() x2+
x2+![]() x+1;
x+1;
(2)当﹣![]() <t<2时,yN>0,
<t<2时,yN>0,
∴NP=|yN|=yN=﹣![]() t2+
t2+![]() t+1,
t+1,
∴S=![]() ABPN
ABPN
=![]() ×(2+
×(2+![]() )×(﹣
)×(﹣![]() t2+
t2+![]() t+1)
t+1)
=![]() (﹣
(﹣![]() t2+
t2+![]() t+1)
t+1)
=﹣![]() t2+
t2+![]() t+
t+![]() ;
;
(3)∵△OPN∽△COB,
∴![]() ,
,
∴![]() ,
,
∴PN=2PO,
当0<t<2时,PN=|yN|=yN=﹣![]() t2+
t2+![]() t+1,PO=|t|=t,
t+1,PO=|t|=t,
∴﹣![]() t2+
t2+![]() t+1=2t,
t+1=2t,
整理得:3t2﹣t﹣2=0,
解得:t1=﹣![]() ,t2=1.
,t2=1.
∵﹣![]() <0,0<1<2,
<0,0<1<2,
∴t=1,此时点N的坐标为(1,2),
故点N的坐标为(1,2).


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
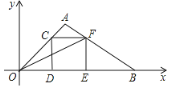
【题目】如图,点A 坐标为(1,1),点C是线段OA上的一个动点(不运动至O,A两点)过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF,连接AF并延长交x轴的正半轴于点B,连接OF,若以B、E、F为顶点的三角形与△OEF相似,,则B的坐标是 ___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在足够大的空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏.
(1)若a=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
(2)求矩形菜园ABCD面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD=BC,点E、F、G、H分别是AB、BD、CD、AC的中点,则四边形EFGH是( )
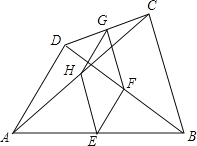
A.矩形B.菱形C.正方形D.平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂要把一批产品从![]() 地运往
地运往![]() 地,若通过铁路运输,则每千米需交运费20元,还要交装卸费400元及手续费200元,若通过公路运输,则每千米需要交运费30元,还需交手续费100元(由于本厂职工装卸,不需交装卸费).设
地,若通过铁路运输,则每千米需交运费20元,还要交装卸费400元及手续费200元,若通过公路运输,则每千米需要交运费30元,还需交手续费100元(由于本厂职工装卸,不需交装卸费).设![]() 地到
地到![]() 地的路程为
地的路程为![]() ,通过铁路运输和通过公路运输需交总运费
,通过铁路运输和通过公路运输需交总运费![]() 元和
元和![]() 元.
元.
(1)求![]() 和
和![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(2)若![]() 地到
地到![]() 地的路程为
地的路程为![]() ,哪种运输可以节省总运费?
,哪种运输可以节省总运费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块铁片边缘是由抛物线和线段AB组成,测得AB=20cm,抛物线的顶点到AB边的距离为25cm.现要沿AB边向上依次截取宽度均为4cm的矩形铁皮,从下往上依次是第一块,第二块…如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是第________块.
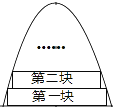
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2017年国内生产总值(GDP)比2016年增长了12%,由于受到国际金融危机的影响,预计2018比2017年增长7%,若这两年GDP年平均增长率为![]() %,则
%,则![]() %满足的关系是( )
%满足的关系是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的“最美数学小报”的评比中,校团委给每个同学的作品打分,成绩分为![]() 四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,将八(1)班与八(2)班的成绩整理并绘制成如下统计图:
四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,将八(1)班与八(2)班的成绩整理并绘制成如下统计图:
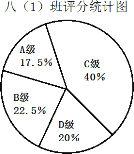

请你根据以上提供的信息解答下列问题:
(1)将表格补充完整.
平均数(分) | 中位数(分) | 众数(分) | |
八(1)班 | 83.75 | 80 | |
八(2)班 | 80 |
(2)若八(1)班有40人,且评分为B级及以上的同学有纪念奖章,请问该班共有几位同学得到奖章?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC分别交AC、AB的延长线于点E、F.
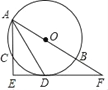
(1)求证:EF是⊙O的切线;
(2)若AC=4,CE=2,求![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com