
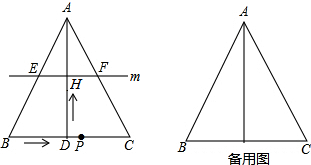
���� ��1�����ͼ1��ʾ���������εĶ���֤����
��2�����ͼ2��ʾ�����������PEF������ı���ʽ��Ȼ�����ö��κ�����������⣮
��� �� 1��֤������t=2ʱ��DH=AH=4����HΪAD���е㣬���ͼ1��ʾ��
1��֤������t=2ʱ��DH=AH=4����HΪAD���е㣬���ͼ1��ʾ��
�֡�EF��AD��
��EFΪAD�Ĵ�ֱƽ���ߣ�
��AE=DE��AF=DF��
��AB=AC��AD��BC�ڵ�D��
��AD��BC����B=��C��
��EF��BC��
���AEF=��B����AFE=��C��
���AEF=��AFE��
��AE=AF��
��AE=AF=DE=DF�����ı���AEDFΪ���Σ�
��2���⣺���ͼ2��ʾ���ɣ�1��֪EF��BC��
���AEF�ס�ABC��
��$\frac{EF}{BC}=\frac{AH}{AD}$����$\frac{EF}{10}=\frac{8-2t}{8}$��
��ã�EF=10-$\frac{5}{2}$t��
S��PEF=$\frac{1}{2}$EF•DH=$\frac{1}{2}$��10-$\frac{5}{2}$t��•2t=-$\frac{5}{2}$t2+10t=-$\frac{5}{2}$��t-2��2+10��0��t��$\frac{10}{3}$����
�൱t=2��ʱ��S��PEF�������ֵ�����ֵΪ10cm2����ʱBP=3t=6cm��
���� �������˶����ۺ��⣬�漰�����붯�������˶����ͣ��ڣ�1���ʿ��������εĶ��壻�ڣ�2���ʿ��������������Ρ�ͼ����������κ����ļ�ֵ���������������ε����ʱ�ʾ��EF�ij��ǽ���Ĺؼ���


 ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д� С��ʿ��ĩ����100��ϵ�д�
С��ʿ��ĩ����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
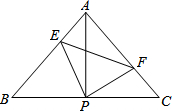 ��֪��ABC�У�AB=AC����BAC=90�㣬ֱ�ǡ�EPF�Ķ���P��BC�е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F�������������ĸ����ۣ�
��֪��ABC�У�AB=AC����BAC=90�㣬ֱ�ǡ�EPF�Ķ���P��BC�е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F�������������ĸ����ۣ�| A�� | �٢� | B�� | �٢� | C�� | �٢ڢ� | D�� | �٢ڢۢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
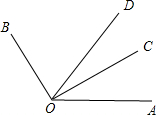 ��ͼ����֪��BOC=2��AOC��ODƽ�֡�AOB���ҡ�AOC=40�㣮
��ͼ����֪��BOC=2��AOC��ODƽ�֡�AOB���ҡ�AOC=40�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{20}=2\sqrt{10}$ | B�� | $\sqrt{9}=��3$ | C�� | $\sqrt{4}-\sqrt{2}=\sqrt{2}$ | D�� | $\sqrt{��-5��^{2}}$=5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��a+b��2=a2+b2 | B�� | a2-b2=��a-b��2 | C�� | ��2x��3=6x3 | D�� | x5��x3=x2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com