
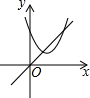
 已知正比例函数y=x与二次函数y=ax2+bx+c的图象如图所示,则二次函数y=ax2+(b-1)x+c的图象可能是( )
已知正比例函数y=x与二次函数y=ax2+bx+c的图象如图所示,则二次函数y=ax2+(b-1)x+c的图象可能是( )| A. |  | B. | 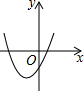 | C. | 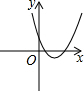 | D. | 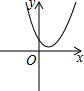 |
分析 由图象可知一次函数y=x与二次函数y=ax2+bx+c交于第一象限的P、Q两点,方程ax2+(b-1)x+c=0有两个正实数根,得到结论.
解答 解:如图,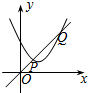
∵点P在抛物线上,设点P(x,ax2+bx+c),又因点P在直线y=x上,
∴x=ax2+bx+c,
∴ax2+(b-1)x+c=0;
由图象可知一次函数y=x与二次函数y=ax2+bx+c交于第一象限的P、Q两点,
∴方程ax2+(b-1)x+c=0有两个正实数根,
∴函数y=ax2+(b-1)x+c的图象与x轴有两个交点,并且这两个交点都在x轴的正半轴上,
符合条件的只有选项C,
故选C.
点评 此题是二次函数图象题,主要考查了正比例函数与二次函数y=ax2+bx+c的图象,以及交点坐标的位置,正确识图是解本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
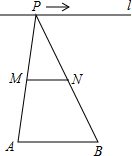 如图,点A,B为定点,定直线l∥AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④∠APB的大小.其中随点P的移动不会变化的是( )
如图,点A,B为定点,定直线l∥AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④∠APB的大小.其中随点P的移动不会变化的是( )| A. | ①② | B. | ②④ | C. | ①③ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+5x+6=0 | B. | x2-5x+6=0 | C. | x2-5x-6=0 | D. | x2+5x-6=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com